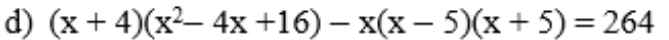K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 8 2018
Ta có \(x.\left(x^2+x+1\right)-x^2.\left(1+x\right)-x-7\)
\(=x^3+x^2+x-x^2-x^3-x-7\)
\(=\left(x^3-x^3\right)-\left(x^2-x^2\right)-\left(x-x\right)-7\)
\(=-7\)
Do đó giá trị của biểu thức không phụ thuộc vào biến
Vậy...
OM
8
KC
1
4 tháng 10 2021
\(\left(x+4\right)\left(x^2-4x+16\right)-x\left(x-5\right)\left(x+5\right)=264\)
\(\Leftrightarrow x^3+64-x^3+25x=264\)
\(\Leftrightarrow25x=200\)
hay x=8
F
23 tháng 1 2020
Bài giải
\(\frac{1}{2}\left(x+1\right)+\frac{1}{4}\left(x+3\right)=3\cdot\frac{1}{3}\cdot\left(x+20\right)\)
\(\frac{1}{2}\left[\left(x+1\right)+\frac{1}{2}\left(x+3\right)\right]=x+20\)
\(\frac{1}{2}\left[x+1+\frac{1}{2}x+\frac{3}{2}\right]=x+20\)
\(\frac{1}{2}\left[x\left(1+\frac{1}{2}\right)+1+\frac{3}{2}\right]=x+20\)
\(\frac{1}{2}\left[\frac{3}{2}x+\frac{5}{2}\right]=x+20\)
\(\frac{3}{4}x+\frac{5}{4}=x+20\)
\(\frac{3}{4}x-x=20-\frac{5}{4}\)
\(\frac{-1}{4}x=\frac{75}{4}\)
\(x=\frac{75}{4}\text{ : }\frac{-1}{4}\)
\(x=-75\)
M
23 tháng 1 2020
\(\frac{1}{2}\left(x+1\right)+\frac{1}{4}\left(x+3\right)=3\cdot\frac{1}{3}\cdot\left(x+20\right)\)
\(\frac{1}{2}\left[\left(x+1\right)+\frac{1}{2}\left(x+3\right)\right]=x+20\)
\(\frac{1}{2}\left[x+1+\frac{1}{2}x+\frac{3}{2}\right]=x+20\)
\(\frac{1}{2}\left[x\left(1+\frac{1}{2}\right)+1+\frac{3}{2}\right]=x+20\)
\(\frac{1}{2}\left[\frac{3}{2}x+\frac{5}{2}\right]=x+20\)
\(\frac{3}{4}x+\frac{5}{4}=x+20\)
\(\frac{3}{4}x-x=20-\frac{5}{4}\)
\(\frac{-1}{4}x=\frac{75}{4}\)
\(x=\frac{75}{4}\text{ : }\frac{-1}{4}\)
\(x=-75\)
8 tháng 10 2021
\(=\left(x^3-2x^2+x+2x^2-4x+2-2x+7\right):\left(x^2-2x+1\right)\\ =\left[\left(x^2-2x+1\right)\left(x+2\right)-2x+7\right]:\left(x^2-2x+1\right)\\ =x+2\left(dư:-2x+7\right)\)
17 tháng 4 2022
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
