K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
20 tháng 5 2016
a. \(a^2+3a-b^2-3b-0\Leftrightarrow\left(a-b\right)\left(a+b+3\right)=0\Leftrightarrow\left[\begin{array}{nghiempt}a=b\\a+b=-3\left(dpcm\right)\end{array}\right.\)
16 tháng 6 2023
3:
a: A(-3;1); B(2;4); C(3;1)
vecto BC=(1;-3)
=>AH có VTPT là (1;-3) và BC có VTPT là (3;1)
PT BC là:
3*(x-2)+1(y-4)=0
=>3x-6+y-4=0
=>3x+y-10=0
PT AH là;
1(x+3)-3(y-1)=0
=>x+3-3y+3=0
=>x-3y+6=0
vecto AC=(6;0)
=>BH có VTPT là (6;0)
Phương trình BH là;
6(x-2)=0
=>x=2
Tọa độ H là;
x=2 và x-3y+6=0
=>x=2 và 8-3y=0
=>H(2;8/3)
b: Tọa độ D là:
x-3y+6=0 và 3x+y-10=0
=>D(12/5;14/5)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
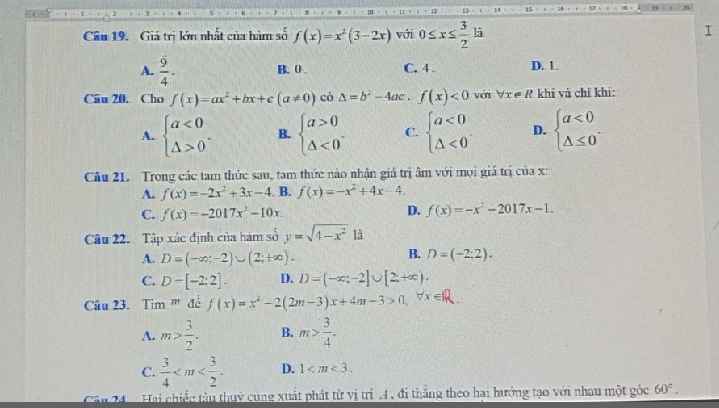
19.
\(f\left(x\right)=x^2\left(3-2x\right)=x.x.\left(3-2x\right)\le\left(\dfrac{x+x+3-2x}{3}\right)^3=1\)
\(\Rightarrow\max\limits_{\left[0;\dfrac{3}{2}\right]}f\left(x\right)=1\)
20.
\(f\left(x\right)< 0;\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a< 0\\\Delta< 0\end{matrix}\right.\)
21.
A là đáp án đúng, do đa thức \(f\left(x\right)=-2x^2+3x-4\) có:
\(\left\{{}\begin{matrix}a=-2< 0\\\Delta=3^2-4.\left(-2\right).\left(-4\right)=-23< 0\end{matrix}\right.\)
22.
ĐKXĐ: \(4-x^2\le0\Rightarrow\left(2-x\right)\left(2+x\right)\le0\)
\(\Rightarrow-2\le x\le2\Rightarrow D=\left[-2;2\right]\)
23.
\(f\left(x\right)>0;\forall x\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=\left(2m-3\right)^2-\left(4m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow4m^2-16m+12< 0\)
\(\Rightarrow1< m< 3\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
Ở đây chỉ thấy các câu 26, 32, 34, 36
26.
\(S_{ABC}=\dfrac{1}{2}AB^2=\dfrac{a^2}{18}\)
\(BC=AB\sqrt{2}=\dfrac{a\sqrt{2}}{3}\Rightarrow p=\dfrac{AB+AC+BC}{2}=\dfrac{2a+a\sqrt{2}}{6}\)
\(\Rightarrow r=\dfrac{S}{p}=\dfrac{6a^2}{18a\left(2+\sqrt{2}\right)}=\dfrac{\left(2-\sqrt{2}\right)a}{6}\)
32.
Đường thẳng nhận \(\overrightarrow{n}=\left(5;-1\right)\) là 1 vtpt
34.
Áp dụng định lý hàm cos:
\(c=\sqrt{a^2+b^2-2ab.cosC}=\sqrt{8^2+7^2-2.8.7.cos60^0}=\sqrt{57}\)
36.
\(y=\sqrt{\dfrac{x^2-2mx+5m}{2021}}\)
Hàm xác định trên R khi và chỉ khi: \(x^2-2mx+5m\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-5m\le0\Rightarrow0\le m\le5\)
Có 5 giá trị nguyên dương của m thỏa mãn (1;2;3;4;5)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2021
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\)
\(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\sqrt{1-\dfrac{9}{16}}=-\dfrac{\sqrt{7}}{4}\)
\(tana=\dfrac{sina}{cosa}=-\dfrac{3\sqrt{7}}{7}\) ; \(cota=\dfrac{1}{tana}=-\dfrac{\sqrt{7}}{3}\)
Bây giờ bạn chỉ cần thay số và bấm máy tính
NL
3
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
15.
\(\Delta'=m^2+m-2>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -2\end{matrix}\right.\)
Đáp án B
16.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow\dfrac{\pi}{4}< \dfrac{a}{2}< \dfrac{\pi}{2}\Rightarrow\dfrac{\sqrt{2}}{2}< sin\dfrac{a}{2}< 1\Rightarrow\dfrac{1}{2}< sin^2\dfrac{a}{2}< 1\)
\(sina=\dfrac{3}{5}\Leftrightarrow sin^2a=\dfrac{9}{25}\Leftrightarrow4sin^2\dfrac{a}{2}.cos^2\dfrac{a}{2}=\dfrac{9}{25}\)
\(\Leftrightarrow sin^2\dfrac{a}{2}\left(1-sin^2\dfrac{a}{2}\right)=\dfrac{9}{100}\Leftrightarrow sin^4\dfrac{a}{2}-sin^2\dfrac{a}{2}+\dfrac{9}{100}=0\)
\(\Rightarrow\left[{}\begin{matrix}sin^2\dfrac{a}{2}=\dfrac{1}{10}< \dfrac{1}{2}\left(loại\right)\\sin^2\dfrac{a}{2}=\dfrac{9}{10}\end{matrix}\right.\)
\(\Rightarrow sin\dfrac{a}{2}=\dfrac{3\sqrt{10}}{10}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
17.
Áp dụng công thức trung tuyến:
\(AM=\dfrac{\sqrt{2\left(AB^2+AC^2\right)-BC^2}}{2}=\dfrac{\sqrt{201}}{2}\)
18.
\(\Leftrightarrow x^2+2x+4>m^2+2m\) ; \(\forall x\in\left[-2;1\right]\)
\(\Leftrightarrow m^2+2m< \min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)\)
Xét \(f\left(x\right)=x^2+2x+4\) trên \(\left[-2;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-2;1\right]\) ; \(f\left(-2\right)=4\) ; \(f\left(-1\right)=3\) ; \(f\left(1\right)=7\)
\(\Rightarrow\min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)=f\left(1\right)=3\)
\(\Rightarrow m^2+2m< 3\Leftrightarrow m^2+2m-3< 0\)
\(\Rightarrow-3< m< 1\Rightarrow m=\left\{-2;-1;0\right\}\)
Đáp án C
NV
2
10 tháng 4 2022
Câu 9: A
Câu 10: C
Câu 11: C
Câu 12: A
Câu 13; B
Câu 14: C
NV
1
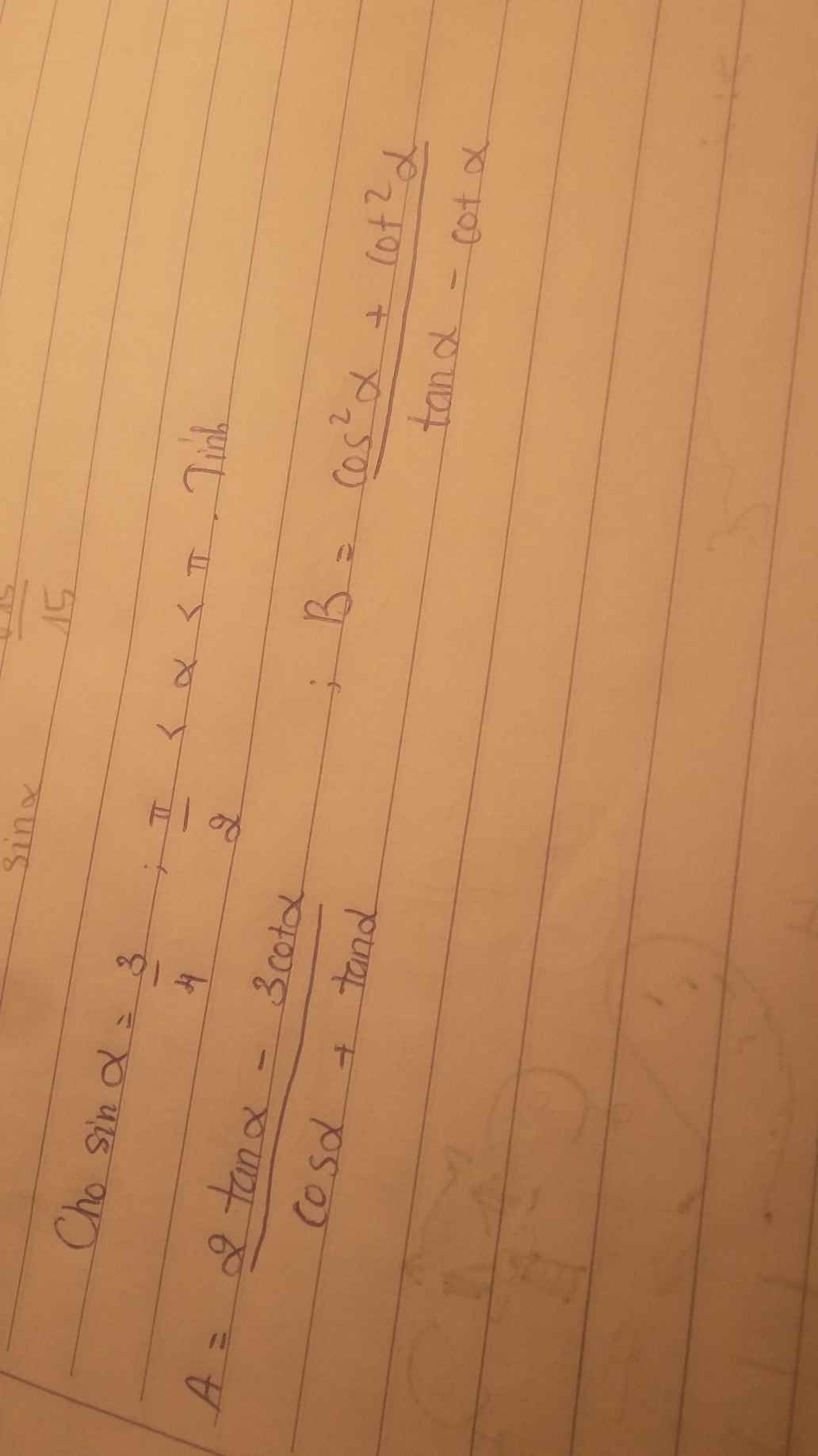
4b. ta có : \(\frac{\left(x_1-1\right)\left(x_2-1\right)-1}{x_1+x_2-2}-\frac{x_1+x_2}{4}\)\(=\frac{x_1x_2-x_1-x_2+1-1}{x_1+x_2-2}-\frac{x_1+x_2}{4}=\frac{x_1x_2-\left(x_1+x_2\right)}{\left(x_1+x_2\right)-2}-\frac{x_1+x_2}{4}\)
Ta có : \(x_1x_2=\frac{c}{a}=m^2+2\) ; \(x_1+x_2=\frac{-b}{a}=2\left(m+1\right)\)
Nên: \(\frac{m^2+2-2\left(m+1\right)}{2\left(m+1\right)-2}-\frac{2\left(m+1\right)}{4}=\frac{m^2+2-2m-2}{2m}-\frac{m+1}{2}=\frac{m^2-2m-m^2-m}{2m}=\frac{-3m}{2m}=\frac{-3}{2}\) \(< 0\) với mọi m .(đpcm)