K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2021
Do tính đối xứng của parabol, \(\Rightarrow H\) là trung điểm AB \(\Rightarrow y_H=y_A=y_B\) đồng thời \(x_A=-x_B\)
Mặt khác \(AB=\left|x_A-x_B\right|=\left|2x_A\right|=4\Rightarrow x_A=2\)
\(\Rightarrow y_A=-x_A^2=-4\Rightarrow y_H=-4\)
\(\Rightarrow OH=\left|y_H\right|=4\) (m)
CM
3 tháng 7 2017
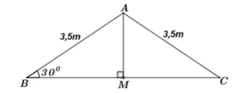
Ta vẽ lại mô hình mái nhà như hình vẽ bên.
Theo đề bài cho ta có: ∆ ABC cân tại A
Thì khi đó bề rộng mái nhà chính là độ dài cạnh BC.
Gọi M là trung điểm của BC.
=> AM là đường trung tuyến đồng thời là đường cao của ABC (tính chất).
Xét ∆ ABM vuông tại M ta có:
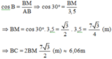
Vậy bề rộng mái nhà là 6,06m
Đáp án cần chọn là: B
