Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này khá quen thuộc rồi. Giải như sau:
Đặt $q_1=Q_0\cos(\omega t_1)\Rightarrow i_1=Q_0\omega\cos(\omega t_1+\frac{\pi}{2})$
Sau $\frac{3T}{4}$: $i_2=Q_0\omega\cos\left ( \omega(t_1+\frac{3T}{4})+\frac{\pi}{2} \right )=Q_0\omega\cos (\omega t_1)$. $(1)$ Mà $i_1=-Q_0\omega\sin (\omega t_1)$
$\Rightarrow i_1^2+i_2^2=I_0^2$ $(\star)$
Áp dụng định luật bảo toàn năng lượng: $Li_2^2+\frac{q_2^2}{C}=LI_0^2$ $(\star \star)$
Từ $(\star), (\star \star)\Rightarrow q_2^2=LCi_1^2=\frac{i_1^2}{\omega ^2}\Rightarrow \omega=4.10^6\pi\rightarrow T=\frac{2\pi}{\omega}=5.10^7=0,5\mu s$

Đáp án C
Phương pháp: Sử dụng vòng tròn lượng giác
Cách giải:
 |
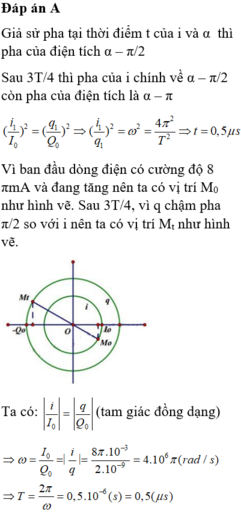
Biểu diễn hai thời điểm như hình vẽ.
Ta có: 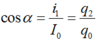
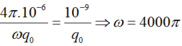
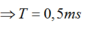
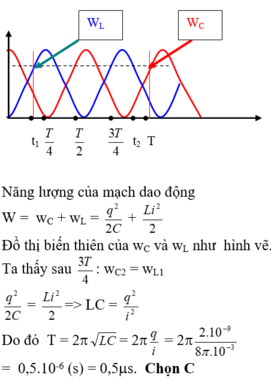

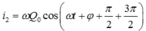
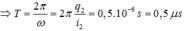
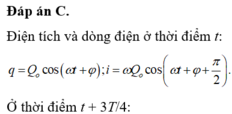
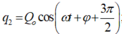
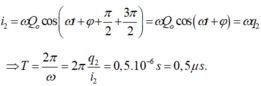

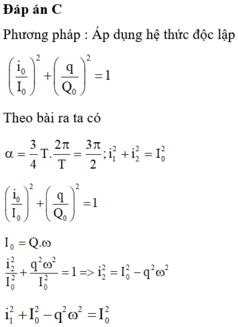
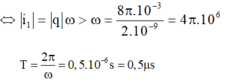
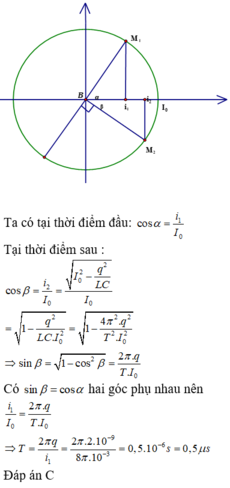
Chọn C
Tại thời điểm t1 bất kỳ, ta luôn có q1 và i1 vuông pha nhau
Tại thời điểm t1 + 3T/4, q1 và q2 vuông pha nhau
Từ (1) và (2)