Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B. Điện trở của dây dẫn giảm đi 10 lần
Áp dụng công thức: 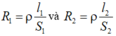
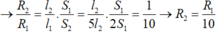

Ta có: \(R=\delta\dfrac{l}{S}\)
Ta thấy rằng tiết diện tỉ lệ nghịch với điện trở dây dẫn nên khi tăng/giảm tiết diện dây đó lên 5 lần thì điện trở sẽ giảm/tăng đi 5 lần.
Điện trở của dây dẫn khi tiết diện tăng là:
\(R_t=\dfrac{R}{5}=2\left(\Omega\right)\)
Điện trở của dây dẫn khi tiết diện giảm là:
\(R_g=5R=50\left(\Omega\right)\)

Theo đề bài, ta có: \(\left\{{}\begin{matrix}\rho=\rho'\\l=l'\\S'=2S\\R=?\end{matrix}\right.\)
Từ công thức \(R=\rho.\dfrac{l}{S}\rightarrow\rho=\dfrac{R.S}{l}\)
\(\rho=\rho'\\ \rightarrow\dfrac{R.S}{l}=\dfrac{R'.S'}{l}\\ \rightarrow R.S=R'.S'\\ \rightarrow R.S=R'.2S'\\ \rightarrow R=2.R'\\ \rightarrow R'=\dfrac{R}{2}\)
Vậy điện trở giảm 1 nửa
\(\rightarrow D\) Giảm đi 2 lần

Đáp án D
Nhiệt tỏa ra là Q = I 2 R . t suy ra nếu đồng thời tăng điện trở của dây dẫn, cường độ dòng điện và thời gian dòng điện chạy qua dây dẫn lên 2 lần thì nhiệt lượng tỏa ra trên dây dẫn sẽ tăng lên 16 lần.

\(\Rightarrow\left\{{}\begin{matrix}I=\dfrac{U}{R}\\I'=\dfrac{U}{3R}\\I-I'=0,6A\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}I=3I'\\3I'-I'=0,6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}I=3.0,3=0,9A\\I'=0,3A\end{matrix}\right.\)\(\Rightarrow I=0,9A\)

Chọn B. vì nhiệt lượng tỏa ra trên dây dẫn: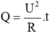
nên khi giảm điện trở đi một nửa thì nhiệt lượng Q tăng gấp đôi.