Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Có 2 trường hợp như sau
+)TH1: có 3 nam, 2 nữ, suy ra có ![]() cách chọn
cách chọn
+) TH2: có 4 nam, 1 nữ, suy ra có ![]() cách chọn
cách chọn
Suy ra xác suất cần tính bằng 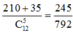

Đáp án A
Chọn 5 học sinh từ đội văn nghệ của nhà trường, ta xét các trường hợp
TH1. 1 học sinh lớp 12A, 2 học sinh lớp 12B và 2 học sinh lớp 12C → có C 4 1 . C 3 2 . C 2 2 = 12 cách.
TH2. 2 học sinh lớp 12A, 1 học sinh lớp 12B và 2 học sinh lớp 12C → có C 4 2 . C 3 1 . C 2 2 = 18 cách
TH3. 3 học sinh lớp 12A, 1 học sinh lớp 12B và 1 học sinh lớp 12C → có C 4 3 . C 3 1 . C 2 1 = 24 cách.
TH4. 1 học sinh lớp 12A, 3 học sinh lớp 12B và 1 học sinh lớp 12C → có C 4 1 . C 3 3 . C 2 1 = 8 cách.
TH5. 2 học sinh lớp 12A, 2 học sinh lớp 12B và 1 học sinh lớp 12C → có C 4 2 . C 3 2 . C 2 1 = 36 cách.

Đáp án B
Chọn 3 đoàn viên trong 20 đoàn viên có C 20 3 cách ⇒ n Ω = C 20 3 .
Gọi X là biến cố “chọn được 3 đoàn viên có ít nhất 1 đoàn viên nữ”
TH1: Chọn được 2 nam và 1 nữ => có C 12 2 . C 8 1 = 528 cách.
TH2: Chọn được 1 nam và 2 nữ => có C 12 1 . C 8 2 = 336 cách.
TH3: Chọn được 0 nam và 3 nữ => có C 12 0 . C 8 3 = 56 cách.
Suy ra số kết quả thuận lợi cho biến có X là n = 528 + 336 + 56 = 920.
Vậy xác suất cần tính là: P = n X n Ω = 920 C 20 3 = 46 57 .

Số cách chọn các bạn đi lao động là:
![]()
Gọi biến cố A: “Chọn mỗi tổ 2 bạn đi lao động, trong đó có đúng 3 bạn nữ”.
Khi đó ta có các TH sau:
+) Tổ 1 có 2 bạn nữ, tổ 2 có 1 bạn nữ và 1 bạn nam có:
![]()
+) Tổ 1 có 1 bạn nữ và 1 bạn nam, tổ 2 có 2 bạn nữ có:
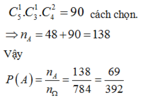
Chọn B.






Đáp án A
C 20 1 . C 16 1 = 320