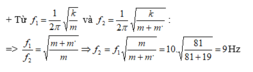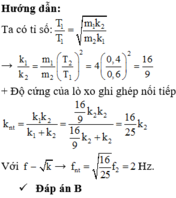Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Chu ki dao đông̣ điều hoa cua con lắc lo xo T = 2 π m k
Cách giải:
Theo bài ra ta có
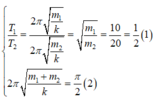
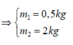

Đáp án C.
Lời giải chi tiết:
Theo giả thiết
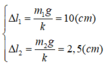
=> Tại vị trí cân bằng của hai vật lò xo dãn 12,5 cm
Thả vật tại vị trí lò xo dãn 20cm =>A=7,5cm
Khi về tới O thì lò xo dãn 10cm =>x = -2,5cm
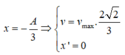
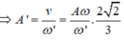
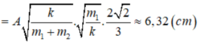

Đáp án D
+ Tại thời điểm ban đầu ta có ∆ l 0 = 10 c m
+ Đưa vật tới vị trí lò xo giãn 20 cm thì có thêm vật m2 = 0,25m1 gắn vào m1 nên khi đó ta sẽ vó VTCB mới O’ dịch xuống dưới so với O 1 đoạn bằng:
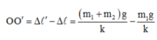

+ Khi về đến O thì m2 tuột khỏi m1 khi đó hệ chỉ còn lại m1 dao động với VTCB O, gọi biên độ khi đó là A1.
+ Vận tốc tại điểm O tính theo biên độ A’ bằng vận tốc cực đại của vật khi có biên độ là A1
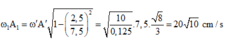
+ Biên độ dao động của m1 sau khi m2 tuột là: A 1 = 20 10 10 0 . 1 = 2 10 ≈ 6 , 32 c m

1. Chu kì 2 vật là:
\(T_1=2\pi\sqrt{\dfrac{m_1}{k_1}}\)
\(T_2=2\pi\sqrt{\dfrac{m_2}{k_2}}\)
Có \(T_1=T_2\)
\(\Rightarrow \dfrac{m_1}{k_1}=\dfrac{m_2}{k_2}\)
\(\Rightarrow \dfrac{k_2}{k_1}=\dfrac{m_2}{m_1}=3\)
Mà với 1 lò xo thì \(k.l=const\)
\(\Rightarrow k_1.l_1=k_2.l_2\)
\(\Rightarrow k_1.CA=k_2.CB\)
\(\Rightarrow \dfrac{k_2}{k_1}=\dfrac{CA}{CB}=3\)
\(\Rightarrow \dfrac{CA}{CA+CB}=\dfrac{3}{3+1}\)
\(\Rightarrow \dfrac{CA}{AB}=\dfrac{3}{4}\)
Tần số dao động:
\(f_1=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m_1}}\)
\(f_2=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m_2}}\)
Ta có: \(\dfrac{f_1}{f_2}=\sqrt{\dfrac{m_2}{m_1}}=\dfrac{10}{5}=2\)
\(\Rightarrow \dfrac{m_1}{m_2}=4\)
Nếu treo cả 2 quả cầu vào lò xo thì chu kì là: \(T=2\pi\sqrt{\dfrac{m_1+m_2}{k}}=2\pi\sqrt{\dfrac{m_1+\dfrac{m_1}{4}}{96}}=\dfrac{\pi}{2}\)
\(\Rightarrow m_1 = 4,8kg\)