
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{6}=\dfrac{x-y}{5-3}=\dfrac{4}{2}=2\)
Do đó: x=10; y=6; z=12
a) Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{6}=\dfrac{x-y}{5-3}=\dfrac{4}{2}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.5=10\\y=2.3=6\\z=2.6=12\end{matrix}\right.\)
b) \(\Rightarrow\dfrac{x}{6}=\dfrac{y}{8}=\dfrac{z}{15}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{8}=\dfrac{z}{15}=\dfrac{2x}{12}=\dfrac{2x+y-z}{12+8-15}=\dfrac{-25}{5}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).6=-30\\y=\left(-5\right).8=-40\\z=\left(-5\right).15=-75\end{matrix}\right.\)

a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: Xét tứ giác CBED có
A là trung điểm của CE
A là trung điểm của BD
Do đó: CBED là hình bình hành
Suy ra: DE//BC

a)\(|a|=\frac{1}{5}\)
\(\Rightarrow\hept{\begin{cases}a=\frac{1}{5}\\a=-\frac{1}{5}\end{cases}}\)
Vậy \(a\in\left\{\frac{1}{5};-\frac{1}{5}\right\}\)


c) \(\frac{x}{y}=\frac{5}{9}\Leftrightarrow\frac{x}{5}=\frac{y}{9}\Leftrightarrow\frac{3x}{15}=\frac{2y}{18};3x+2y=66\)
Tính chất dãy tỉ số bằng nhau:
\(\frac{3x}{15}=\frac{2y}{18}=\frac{3x+2y}{15+18}=\frac{66}{33}=2\)
\(\Rightarrow\hept{\begin{cases}\frac{3x}{15}=2\Leftrightarrow x=\frac{15.2}{3}=10\\\frac{2y}{18}=2\Leftrightarrow y=\frac{18.2}{2}=18\end{cases}}\)
d) \(\frac{x}{15}=\frac{y}{7}\Leftrightarrow\frac{x}{15}=\frac{2y}{14};x-2y=16\)
Tính chất dãy tỉ số bằng nhau:
\(\frac{x}{15}=\frac{2y}{14}=\frac{x-2y}{15-14}=\frac{16}{1}=16\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{15}=16\Leftrightarrow x=240\\\frac{2y}{14}=16\Leftrightarrow y=\frac{14.16}{2}=112\end{cases}}\)
e) \(\frac{x}{5}=\frac{y}{2};xy=1000\)
Đặt \(\frac{x}{5}=\frac{y}{2}=k\)
\(\Rightarrow\hept{\begin{cases}x=5k\\y=2k\end{cases}}\)
Mà \(xy=1000\)
\(\Rightarrow5k.2k=1000\)
\(\Rightarrow10k^2=1000\)
\(\Rightarrow k^2=100\)
\(\Rightarrow\orbr{\begin{cases}k=10\\k=-10\end{cases}}\)
Với \(k=10\Rightarrow\hept{\begin{cases}x=5.10=50\\y=2.10=20\end{cases}}\)
Với \(k=-10\Rightarrow\hept{\begin{cases}x=5.\left(-10\right)=-50\\y=2.\left(-10\right)=-20\end{cases}}\)

ba ý đầu mị lm ntn này nek, coi đúng hông ha^^
a)xét tam giác vuông ABD và tam giác vuônng có: AB=AD(gt); A chung
=>ABD=ACE(ch-gn)
ý b bỏ ha, lm ý c
AE=AD(tam giác ABD=ACE)=>Tam giác AED cân tại A
=>\(\widehat{AED}=\widehat{ADE}=\frac{180-\widehat{EAD}}{2}\left(1\right)\)
xét tam giác ABC cân tại A:
=>\(\widehat{ABC}=\widehat{ACB}=\frac{180-\widehat{BAC}}{2}hay:\widehat{EBC}=\widehat{DCB}=\frac{180-\widehat{EAD}}{2}\left(2\right)\)
Từ (1) và (2) => góc AED=EBC
mak hay góc mày ở vtris đồng vị nên ED//BC
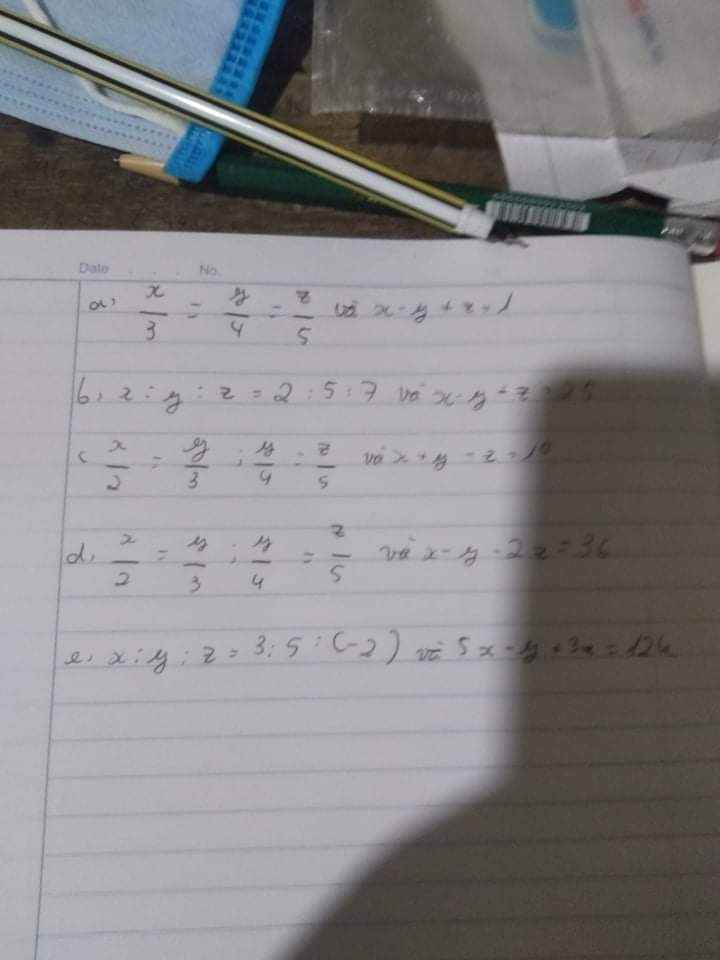
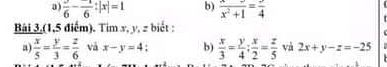

b, Áp dụng t/c dtsbn:
\(x:y:z=2:5:7\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{x-y+z}{2-5+7}=\dfrac{25}{4}\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{25}{2}\\y=\dfrac{125}{4}\\z=\dfrac{175}{4}\end{matrix}\right.\)
c, Áp dụng t/c dstbn:
\(\dfrac{x}{2}=\dfrac{y}{3};\dfrac{y}{4}=\dfrac{z}{5}\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\\ \Rightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\)
d, Áp dụng t/c dstbn:
\(\dfrac{x}{2}=\dfrac{y}{3};\dfrac{y}{4}=\dfrac{z}{5}\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x-y-2z}{8-12-2\cdot15}=\dfrac{36}{-34}=-\dfrac{18}{17}\\ \Rightarrow\left\{{}\begin{matrix}x=-\dfrac{144}{17}\\y=-\dfrac{216}{17}\\z=-\dfrac{270}{17}\end{matrix}\right.\)
e, Áp dụng t/c dtsbn:
\(x:y:z=3:5:\left(-2\right)\Rightarrow\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{-2}=\dfrac{5x-y+3z}{3\cdot5-5+3\left(-2\right)}=\dfrac{12}{4}=3\\ \Rightarrow\left\{{}\begin{matrix}x=9\\y=15\\z=-6\end{matrix}\right.\)