Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ta có ![]()
Gọi số tự nhiên cần tìm có bốn chữ số là a b c d ¯
Vì a b c d ¯ chia hết cho 11 nên (a + c) - (b + d) ⋮ 11
=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do
![]()
![]()
Theo đề bài ta cũng có a + b + c + d chia hết cho 11
Mà ![]()
![]()
![]()
![]() hoặc
hoặc ![]()
Vì ![]()
![]() nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ
nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ

![]()
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:
![]()
- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2 cách.
- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.
![]()
Vậy xác suất cần tìm là 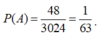

Số các số có `8` chữ số đôi một khác nhau là `9.A_9^7`(số)
`=> n(A) = n(\Omega) = 9.A_9^7`
Dễ thấy rằng `0 + 1 + 2 + .. + 9 = 45 \vdots 9`
Gọi `X = {0;1;..;9}`
Để số đó chia hết cho `8` thì nó phải được chọn từ các tập
`X \\ {0;9}` , `X \\ {1;8}` , `X \\ {2;7}` , `X \\ {3;6}` , `X \\ {4;5}`
Ta xét `2` trường hợp như sau:
Trường hợp `1`: Số đó được chọn từ tập `X \\ {0;9}`
Xếp `8` số vào `8` vị trí có `8!`(cách)
Trường hợp `2`:Số đó được chọn từ `4` tập còn lại
Chọn `1` trong `4` tập có `C_4^1`(cách)
Xếp `8` chữ số vừa chọn `1` cách ngẫu nhiên có `8!`(cách)
Cho số `0` đứng đầu xếp `7` số còn lại có `7!` cách
Số lập được:`4(8!-7!)`(số)
Gọi `B` là biến cố chọn được số chia hết cho `9` từ tập `A`
`=> |B| = 8! + 4(8!-7!)`
Xác xuất biến cố `B`:
`P(B) = \frac{8!+4(8!-7!)}{9.A_9^7} = \frac{1}{9}`

Cách chọn số đầu tiên : 7 cách
Cách chọn số thứ 2: 7 cách
=> Không gian mẫu: \(n\left(\Omega\right)=7.7=49\)
a/ Gọi số chẵn là \(\overline{ab}\)
Xét b=0 => Có 1 cách chọn b và 7 cách chọn a
Xét b= 2;4;6=> có 3 cách chọn b và 6 cách chọn a
=> Có 1.7+3.6=25 (số chẵn)
=> \(n\left(A\right)=25\Rightarrow p\left(A\right)=\dfrac{25}{49}\)
b/ Gọi số chia hết cho 5 có dạng \(\overline{cd}\)
Xét d=0 => Có 1 cách chọn d và 7 cách chọn c
Xét d=5 => Có 1 cách chọn d và 6 cách chọn c
=> Có 1.7+ 1.6=13 (số chia hết cho 5)
\(\Rightarrow n\left(B\right)=13\Rightarrow p\left(B\right)=\dfrac{13}{49}\)
c/ Các số chia hết cho 9 có dạng \(\overline{ef}\)
\(e+f=9\Rightarrow\left(e;f\right)=\left(2;7\right);\left(3;6\right);\left(4;5\right)\)
\(\Rightarrow co:2!.3=6\left(so-chia-het-cho-9\right)\)
\(\Rightarrow n\left(C\right)=6\Rightarrow p\left(C\right)=\dfrac{6}{49}\)

Chọn A
Giả sử số cần lập là ![]()
Số phần từ không gian mẫu: ![]()
Gọi A là biến cố lấy được số chia hết cho 11 và tổng của các chữ số của chúng cũng chia hết cho 11.
Ta có:
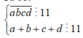
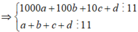
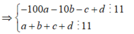
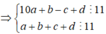
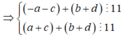
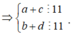
Từ 1,2,3,4,5,6,7,8,9 ta có 4 cặp tổng chia hết cho 11 là: ![]()
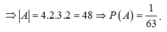

Èo toàn bài khó nhằn :( Thôi làm được mỗi câu 2, câu 1 thì...dẹp đi
\(n\left(\Omega\right)=9.9.8.7.6.5\)
Số lẻ vậy thì f={1;3;5;7;9}
Nhưng nếu f=1 thì ko tồn tại a thỏa mãn a<f do a khác 0
f=3 cũng ko thỏa mãn do nếu a=1; b=2; nhưng ko tồn tại c thỏa mãn :v
f=5 tương tự, ko tồn tại e thỏa mãn
=> f={7;9}
Nếu f=7 thì (a,b,c,d,e)={1;2;3;4;5;6} và chỉ có duy nhất 1 cách sắp xếp \(\Rightarrow C^5_6\left(cach\right)\)
Nếu f=9 thì (a,b,c,d,e)={1;2;3;4;5;6;7;8} và chỉ có duy nhất một cách xếp \(\Rightarrow C^5_8\left(cach\right)\)
\(\Rightarrow n\left(A\right)=C^5_6+C^5_8\) \(\Rightarrow p\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)
Gọi A là số tự nhiên có 8 chữ số a1a2a3a4a5a6a7a8 chia hết cho 1111
9999a1a2a3a4 + a1a2a3a4+a5a6a7a8 để A chia hết cho 1111 thì a1a2a3a4+a5a6a7a8 chia hết cho 1111
1000(a1 + a5) + 100(a2 + a6) + 10(a3 + a7) + (a4+ a8) (1) chia hết cho 1111
đặt (a1 + a5) = x
(a2 + a6) = y
(a3 + a7) = z
(a4+ a8) = t
3<=x<=15
xét đk
suy ra x = 9
suy ra x=y=z=t= 9
suy ra x+y+z+t=36 suy ra t= 36-x-y-z
thế vào (1) suy ra
999(a1 + a5) + 99(a2 + a6) + 9(a3 + a7) =36
hoán vị .......
suy ra có 3840 số
Chọn B
Ta có: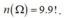
Ta thấy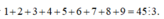
Ta chon 9 số không có số 0 thì được 9! cách.
Ta Chọn có số 0 thì trong dãy số phải bỏ ra 3 hoặc 6 hoặc 9 nên có 3.8.8! cách
Do đó
Vậy P(A) = 11 27