Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu Ω={1,2,..30}. kí hiệu A là biến cố “ thẻ lấy ra ghi số 6”, B là biến cố “thẻ lấy ra ghi số chia hết cho 5”
A={6}, n(A) =1,n(Ω) = 30
⇒P(A) =1/30
Chọn đáp án A

Đáp án D
Các trường hợp thẻ lấy thỏa mãn đề bài là 3, 9, 15
Suy ra xác suất lấy được thẻ đó là 3 20 = 0 , 15 .

Gọi T là biến cố "Lấy được thẻ có ghi số chia hết cho 3".
\(\left|\Omega\right|=C^2_{17}\)
TH1: Lấy được 1 thẻ có ghi số chia hết cho 3.
\(\Rightarrow\) Có \(C^1_5.C^1_{12}\) cách lấy.
TH2: Lấy được 2 thẻ có ghi số chia hết cho 3.
\(\Rightarrow\) Có \(C^2_5\) cách lấy.
\(\Rightarrow\left|\Omega_T\right|=C^1_5.C^1_{12}+C^2_5\)
\(\Rightarrow P\left(T\right)=\dfrac{\left|\Omega_T\right|}{\left|\Omega\right|}=\dfrac{C^1_5.C^1_{12}+C^2_5}{C^2_{17}}=\dfrac{35}{68}\)

gọi\(\Omega\) là không gian mẫu để rút ra 10 tấm thẻ trong 30 tấm==>n(\(\Omega\))=C1030 =30045015
gọi A là biến cố "lấy 10 tấm thẻ trong đó có 5 tấm mang số lẻ, 5 tấm chẵn trong đó có 1 tấm chia hết cho 10"
nx: có 30 tấm đánh số từ 1->30 ------->15 tấm lẻ, 15 tấm chẵn, có 3 tấm chứa số 10, 20,30 là chia hết cho 10
- trường hợp rút 5 tấm lẻ là :C515 =3003 cách
- TH rút 5 tấm chẵn trong đó có 1 tấm chia hết cho 10 là
3xC412 =1485 cách
=======> n(A)=1485x3003=4459455 cách====>P(A)=99/667

Đáp án A
Chọn 10 tấm bất kì có C 30 10
trong 30 thẻ có 15 thẻ mang số chẵn
15 thẻ mang số lẻ và 3 số chia hết cho 10
Ta chọn 10 tấm thẻ lấy ra có 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn
trong đó chỉ có 1 tấm mang số chia hết cho 10 có
![]()
Do đó xác suất cần tìm là
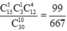

Đáp án A
Chọn 10 tấm bất kỳ có: C 30 10 , trong 30 thẻ có 15 thẻ mang số chẵn, 15 thẻ mang số lẻ và 3 số chia hết cho 10.
Ta chọn 10 tấm thẻ lấy ra 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó chỉ có một tấm mang số chia hết cho 10 có: C 15 5 . C 3 1 . C 12 4 cách
Do đó xác suất cần tìm là: C 15 5 . C 3 1 . C 12 4 C 30 10 = 99 667 .



B = {5,10,15,20,25,30}, n(B) = 6
⇒P(B) =6/30 =1/5
Chọn đáp án là B
Nhận xét: học sinh có thể nhầm với số thẻ và số ghi trên thẻ, hoặc vận dụng nhầm công thức P(A) =(n(Ω))/(n(A)) dẫn đến các phương án khác còn lại.