K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
11 tháng 6 2017
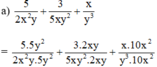
(Quy đồng với MTC = 10x2y3)
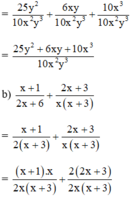
(Quy đồng với MTC = 2x(x + 3))
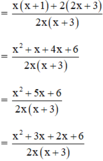
(Tách 5x = 2x + 3x để phân tích tử thành nhân tử)
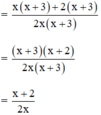
(Rút gọn nhân tử chung x + 3)
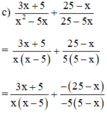
(Áp dụng quy tắc đổi dấu)
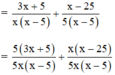
(Quy đồng với MTC = 5x(x – 5))
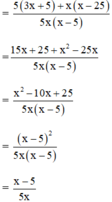
(Rút gọn nhân tử chung x – 5)
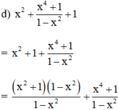
(Quy đồng với MTC = 1 – x2)
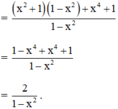
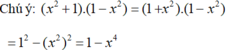
(hằng đẳng thức đáng nhớ số 3: a2 – b2 = (a - b).(a+ b)
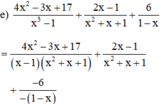
(Phân tích mẫu thức thứ nhất thành nhân tử, áp dụng quy tắc đổi dấu ở phân thức thứ ba)
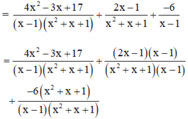
(Quy đồng với MTC = (x – 1)(x2 + x + 1))
11 tháng 1 2022
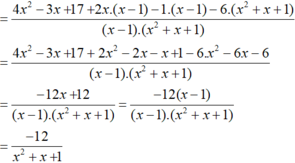
\(=\dfrac{2x-3y}{y\left(x-y\right)}+\dfrac{1}{x-y}=\dfrac{2x-3y+y}{y\left(x-y\right)}=\dfrac{2x-2y}{y\left(x-y\right)}=\dfrac{2}{y}\)
11 tháng 1 2022
\(\dfrac{2x-3y}{xy-y^2}+\dfrac{1}{x-y}=\dfrac{2x-3y}{y\left(x-y\right)}+\dfrac{1}{x-y}=\dfrac{2x-3y+y}{y\left(x-y\right)}=\dfrac{2x-2y}{y\left(x-y\right)}=\dfrac{2}{y}.\)
CM
23 tháng 2 2019
- Qui tắc cộng hai phân thức cùng mẫu:
Muốn cộng hai phân thức có cùng mẫu thức, ta cộng các tử thức với nhau và giữ nguyên mẫu thức.
- Qui tắc cộng hai phân thức khác mẫu:
Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.
- Làm tính cộng:
PT
1
CM
22 tháng 7 2017
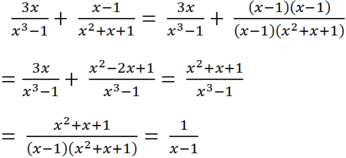
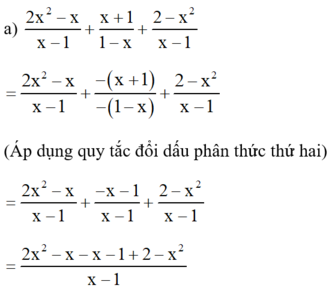
(Cộng các tử thức với nhau, giữ nguyên mẫu thức)
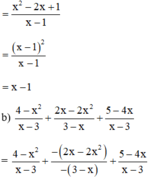
(Áp dụng quy tắc đổi dấu phân thức thứ hai)
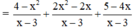
(Cộng các phân thức cùng mẫu thức)
PT
1
PT
1
PT
1
PT
1
PT
1
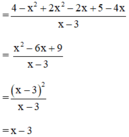
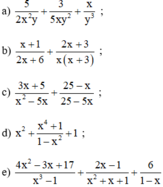
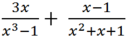
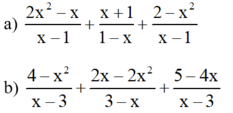
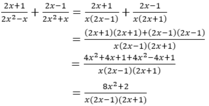
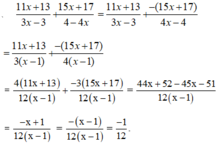
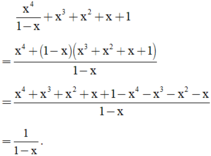
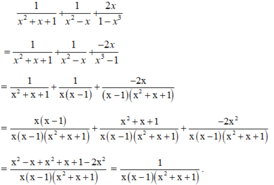
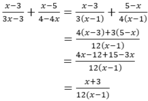
f: \(=\dfrac{x^2+2+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)