Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

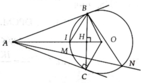
a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC

Vì \(\widehat{ABO}\)là góc tạo bởi tia tiếp tuyến AB và dây cung BD ( đường kính AB )
\(\Rightarrow\widehat{ABO}=\frac{1}{2}.\widehat{BOD}=\frac{1}{2}.180^o=90^o\)
Chứng mình ương tự với \(\widehat{ACO}\), suy ra \(\widehat{ACO}=90^o\)
Xét tứ giác ABOC có :
Góc ABO và góc ACO là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=90^o+90^o=180^o\)
=> Tứ giác ABOC nội tiếp đường tròn ( theo tính chất tổng hai góc đối bằng 180 độ ... )
Gọi I là trung điểm của AB
Có tam giác ABO vuông tại B, trung tuyến là BI
=> BI = 1/2.AO=AI=IO (1)
Tam giác ACO vuông tại C, có trung tuyến là CI
=> CI=1/2.AO=AI=IO (2)
Từ (1) và (2) => BI = AI = IO = IC
=> I cách đều 4 đỉnh tứ giác ABOC
=> I là tâm đường tròn ngoại tiếp tứ giác ABOC , có bán kinh R= 1/2.AO


a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
A B O ^ = 90 0 A C O ^ = 90 0 A B O ^ + A C O ^ = 180 0
=> tứ giác ABOC nội tiếp được đường tròn.
b) Vẽ cát tuyến ADE của (O) sao cho ADE nằm giữa 2 tia AO, AB; D, E Î (O) và D nằm giữa A, E. Chứng minh A B 2 = A D . A E .
Tam giác ADB đồng dạng với tam giác ABE
⇒ A B A E = A D A B ⇔ A B 2 = A D . A E
c) Gọi F là điểm đối xứng của D qua AO, H là giao điểm của AO và BC. Chứng minh: ba điểm E, F, H thẳng hàng.
Ta có D H A ^ = E H O ^
nên D H A ^ = E H O ^ = A H F ^ ⇒ A H E ^ + A H F ^ = 180 0 ⇒ 3 điểm E, F, H thẳng hàng.
Có 1 phần câu trả lời ở đây.
Giải toán: Bài hình trong đề thi HK2 Lớp 9 | Rất phức tạp. - YouTube