
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 4:
a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó:NP là đường trung bình của ΔBCD
Suy ra: NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
hay MQPN là hình bình hành

Bài 2:
c: \(=\left(x+y\right)^2-49\)
\(=\left(x+y+7\right)\left(x+y-7\right)\)


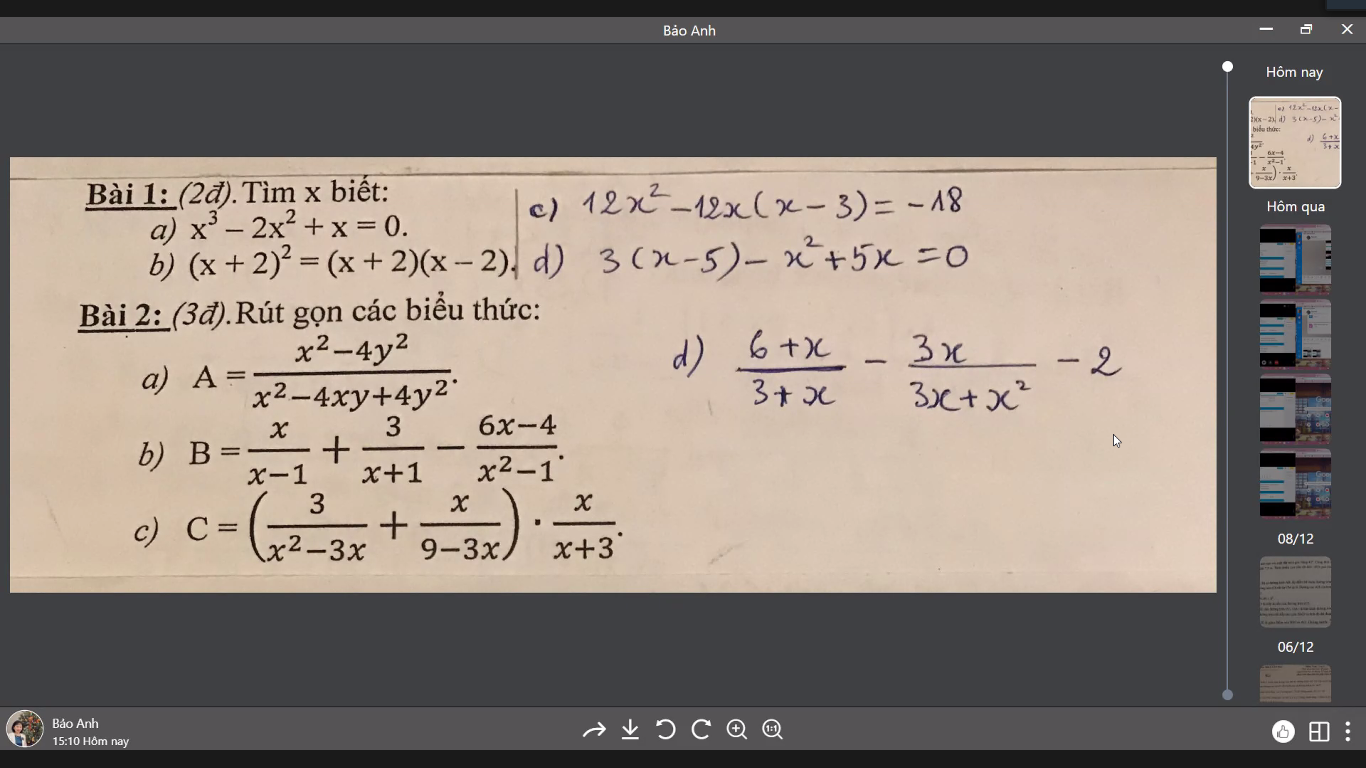
Bài 1
\(x^3-2x^2+x=0\\ \Leftrightarrow x\left(x^2-2x+1\right)=0\\ \Leftrightarrow x\left(x-1\right)^2=0\)
\(\Leftrightarrow x=0\) hoặc \(\left(x-1\right)^2=0\\ \Leftrightarrow x-1=0\\ \Leftrightarrow x=1\)
\(\left(x+2\right)^2=\left(x+2\right)\left(x-2\right)\\ \Leftrightarrow\left(x+2\right)^2-\left(x+2\right)\left(x-2\right)=0\\ \Leftrightarrow\left(x+2\right)\left(x+2-x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)4=0\\ \Leftrightarrow4x+8=0\\ \Leftrightarrow4x=-8\\ \Leftrightarrow x=-\dfrac{8}{4}\\ \Leftrightarrow x=-2\)

c: \(3x\left(x-7\right)-2\left(x-7\right)=0\)
\(\Leftrightarrow\left(x-7\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=\dfrac{2}{3}\end{matrix}\right.\)
d: \(7x^2-28=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

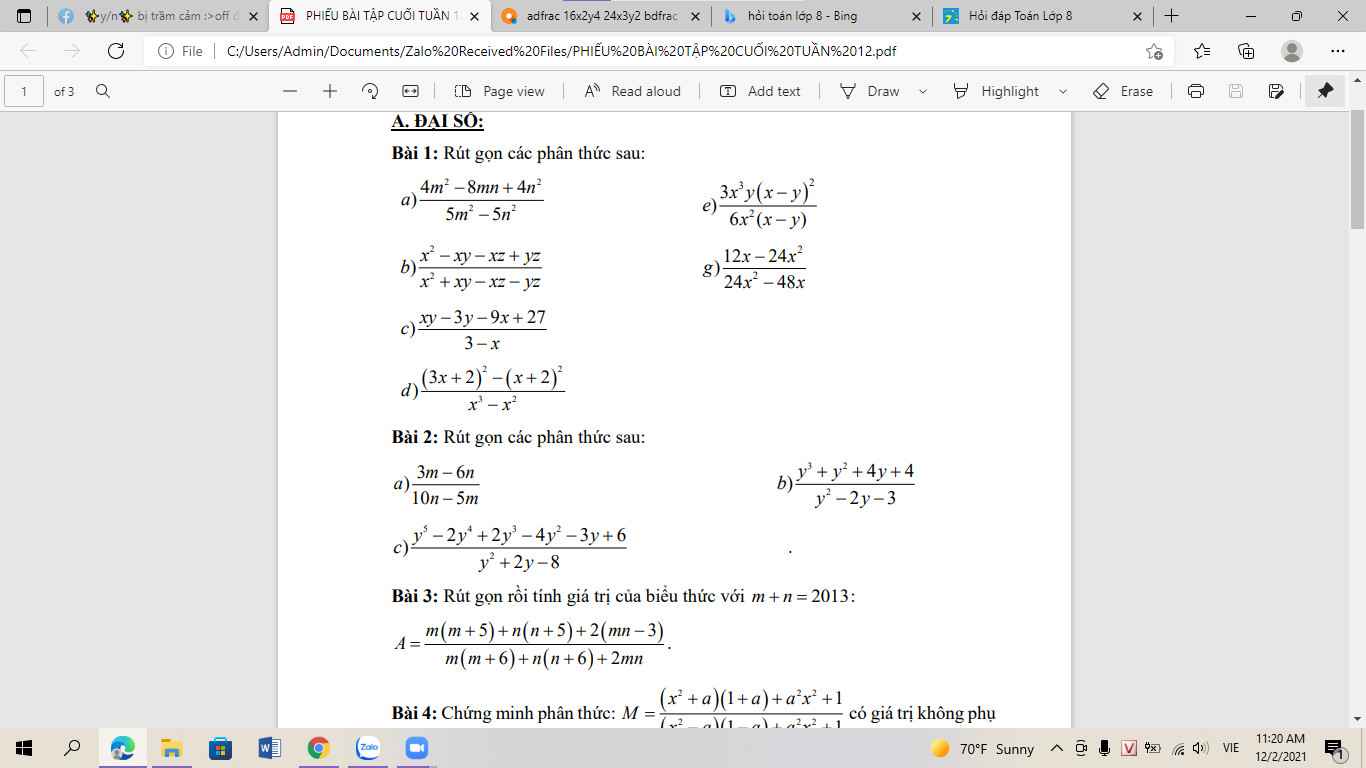
Bài 1:
a) \(=\dfrac{\left(2m-2n\right)^2}{5\left(m^2-n^2\right)}=\dfrac{4\left(m-n\right)^2}{5\left(m-n\right)\left(m+n\right)}=\dfrac{4m-4n}{4m+5n}\)
b) \(=\dfrac{\left(x-y\right)\left(x-z\right)}{\left(x+y\right)\left(x-z\right)}=\dfrac{x-y}{x+y}\)
c) \(=\dfrac{\left(x-3\right)\left(y-9\right)}{-\left(x-3\right)}=9-y\)
d) \(=\dfrac{\left(3x+2-x-2\right)\left(3x+2+x+2\right)}{x^2\left(x-1\right)}=\dfrac{8x\left(x+1\right)}{x^2\left(x-1\right)}=\dfrac{8x+8}{x^2-x}\)
e) \(=\dfrac{xy\left(x-y\right)}{2}=\dfrac{x^2y-xy^2}{2}\)
g) \(=\dfrac{12x\left(1-2x\right)}{24x\left(x-2\right)}=\dfrac{1-2x}{2x-4}\)
Bài 2:
a) \(=\dfrac{3\left(m-2n\right)}{-5\left(m-2n\right)}=-\dfrac{3}{5}\)
b) \(=\dfrac{\left(y+1\right)\left(y^2+4\right)}{\left(y-3\right)\left(y+1\right)}=\dfrac{y^2+4}{y-3}\)
c) \(=\dfrac{y^4\left(y-2\right)+2y^2\left(y-2\right)-3\left(y-2\right)}{\left(y-2\right)\left(y+4\right)}=\dfrac{\left(y-2\right)\left(y^4+2y^2-3\right)}{\left(y-2\right)\left(y+4\right)}=\dfrac{y^4+2y^2-3}{y+4}\)
Bài 3:
\(A=\dfrac{\left(m^2+2mn+n^2\right)+5\left(m+n\right)-6}{\left(m^2+2mn+n^2\right)+6\left(m+n\right)}=\dfrac{\left(m+n\right)^2+5\left(m+n\right)-6}{\left(m+n\right)^2+6\left(m+n\right)}=\dfrac{2013^2+5.2013-6}{2013^2+6.2013}=\dfrac{2012}{2013}\)










chữ nhỏ thế tui làm sao làm được
phóng to ra