K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Lời giải:
a.
$4x=3y\Rightarrow 20x=15y$
$5y=3z\Rightarrow 15y=9z$
$\Rightarrow 20x=15y=9z=t$
$\Rightarrow x=\frac{t}{20}; y=\frac{t}{15}; z=\frac{t}{9}$
Khi đó:
$2x-3y+z=\frac{2t}{20}-\frac{3t}{15}+\frac{t}{9}=5$
$\frac{t}{90}=6$
$t=540$
$x=\frac{540}{20}=27; y=\frac{540}{15}=36;z=\frac{540}{9}=60$
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
b. Đặt $5x=8y=3z=t$
$\Rightarrow x=\frac{t}{5}; y=\frac{t}{8}; z=\frac{t}{3}$
Khi đó:
$x-2y+z=34$
$\frac{t}{5}-\frac{2t}{8}+\frac{t}{3}=34$
$\frac{17}{60}t=34$
$t=120$
$x=\frac{120}{5}=24; y=\frac{120}{8}=15; z=\frac{120}{3}=40$
c.
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$
$\Rightarrow x=2t; y=3t; z=4t$
Khi đó:
$x^2+3y^2-2z^2=-16$
$(2t)^2+3(3t)^2-2(4t)^2=-16$
$-t^2=-16$
$t^2=16$
$t=\pm 4$
Khi $t=4$ thì $x=2.4=8; y=3.4=12; z=4.4=16$
Khi $t=-4$ thì $x=-8; y=-12; z=-16$
AH
Akai Haruma
Giáo viên
4 tháng 8 2021
Bài 1:
a. $x:(\frac{-5}{9})^8=(\frac{-9}{5})^8$
$x=(\frac{-9}{5})^8.(\frac{-5}{9})^8=(\frac{-9}{5}.\frac{-5}{9})^8=1^8$
$x=1$
b. $(x+5)^3=-27=(-3)^3$
$x+5=-3$
$x=-8$
c.
$(2x+5)^4=4096=8^4=(-8)^4$
$\Rightarrow 2x+5=8$ hoặc $2x+5=-8$
$\Leftrightarrow x=\frac{3}{2}$ hoặc $x=-\frac{13}{2}$
d. $3^{x+1}=243=3^5$
$\Leftrightarrow x+1=5$
$\Leftrightarrow x=4$
e.
$\frac{-32}{(-2)^x}=4$
$(-2)^x=-8=(-2)^3$
$\Leftrightarrow x=3$
f.
$7^{x+2}+2.7^{x-1}=345$
$7^{x-1}(7^3+2)=345$
$7^{x-1}.345=345$
$7^{x-1}=1=7^0$
$\Rightarrow x-1=0\Leftrightarrow x=1$
AH
Akai Haruma
Giáo viên
4 tháng 8 2021
Bài 2:
Ta thấy:
$2^{30}=(2^3)^{10}=8^{10}< 9^{10}=(3^2)^{10}=3^{20}$
Vậy $2^{30}< 3^{20}$
-------------------------
$5^{202}$ và $2^{505}$
$5^{202}=(5^2)^{101}=25^{101}< 32^{101}=(2^5)^{101}=2^{505}$
Vậy $5^{202}< 2^{505}$
NT
1
NN
16 tháng 10 2017
Tính phần tử số:
101+100+99+...+2+1
=\(\dfrac{\left(101+1\right).101}{2}\)=5151
Phần mẫu số:
101-100+99-98+...+2-1+1
=1+1+...+1+1 ( 51 số 1 )
= 51
Thay vào biểu thức, ta có:
\(\dfrac{5151}{51}\)=101
Chúc bạn học tốt nhé :))!!
LP
2
12 tháng 9 2016
Giai
a, Với x>=5 thì ta có xpt: x-5 -3x=3 => -2x-5=3 => x=-4 (loại vì x bé hơn 5)
Với x<5 thì ta có pt : 5-x-3x=3 => 5-4x =3 =>x=1\2 (t\m)
Vây x=1\2
b, Tương tụ nha pn...nhớ k nha
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)
TT
1
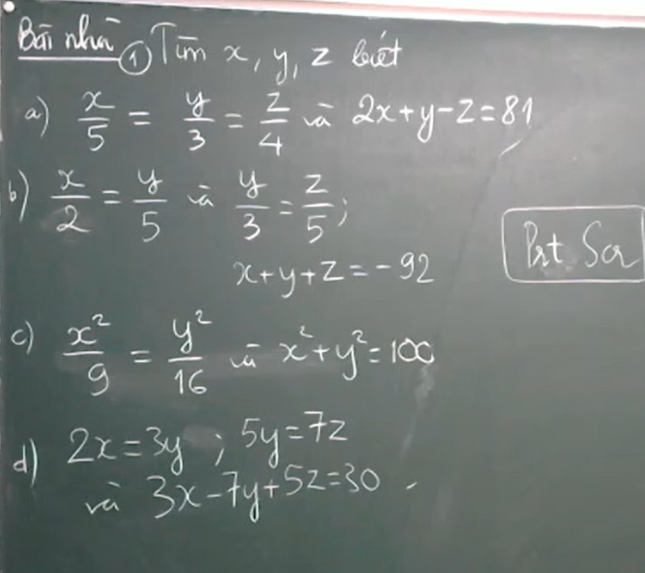
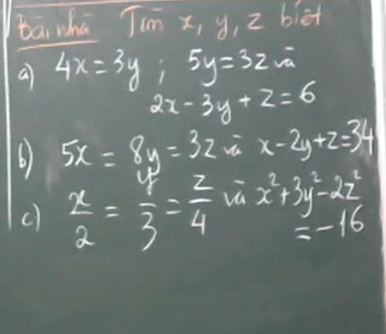
a) Ta có:
\(\dfrac{x}{5}=\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{10+3-4}=\dfrac{81}{9}=9\\ \Rightarrow\left\{{}\begin{matrix}x=9\cdot5=45\\y=9\cdot3=27\\z=9\cdot4=36\end{matrix}\right.\)
Vậy x = 45; y = 27; z = 36.
b) Ta có:
\(\dfrac{x}{2}=\dfrac{y}{5}\)\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{15}\)
\(\dfrac{y}{3}=\dfrac{z}{5}\)\(\Rightarrow\dfrac{y}{15}=\dfrac{z}{25}\)
suy ra, \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{6+15+25}=-\dfrac{92}{46}=-2\\ \Rightarrow\left\{{}\begin{matrix}x=-2\cdot6=-12\\y=-2\cdot15=-30\\z=-2\cdot25=-50\end{matrix}\right.\)
Vậy x = -12; y = -30; z = -50.
c) Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=4\\ \Rightarrow\left\{{}\begin{matrix}x^2=36\\y^2=64\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=6\\y=8\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=8\end{matrix}\right.\\\left\{{}\begin{matrix}x=6\\y=-8\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=-8\end{matrix}\right.\end{matrix}\right.\)
Vậy (x; y) \(\in\left\{\left(6;8\right);\left(-6;8\right);\left(6;-8\right);\left(-6;-8\right)\right\}\)
d), Ta có:
\(2x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}\\ 5y=7z\Rightarrow\dfrac{y}{7}=\dfrac{z}{5}\Rightarrow\dfrac{y}{14}=\dfrac{z}{10}\\ \Rightarrow\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\\ \Rightarrow\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}=\dfrac{3x-7y+5z}{63-98+50}=\dfrac{30}{15}=2\\ \Rightarrow\left\{{}\begin{matrix}x=2\cdot21=42\\y=2\cdot14=28\\z=2\cdot10=20\end{matrix}\right.\)
Vậy x = 42; y = 28; z = 20.
a: Ta có: \(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{4}\)
nên \(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{10+3-4}=\dfrac{81}{9}=9\)
Do đó: x=45; y=27; z=36
b: Ta có: \(\dfrac{x}{2}=\dfrac{y}{5}\)
nên \(\dfrac{x}{6}=\dfrac{y}{15}\left(1\right)\)
Ta có: \(\dfrac{y}{3}=\dfrac{z}{5}\)
nên \(\dfrac{y}{15}=\dfrac{z}{25}\left(2\right)\)
Từ (1), (2) suy ra \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}\)
mà x+y+z=-92
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{6+15+25}=-\dfrac{92}{46}=-2\)
Do đó: x=-12; y=-30; z=-50
c: Ta có: \(\dfrac{x^2}{9}=\dfrac{y^2}{16}\)
mà \(x^2+y^2=100\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
Do đó: \(\left\{{}\begin{matrix}x^2=36\\y^2=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{6;-6\right\}\\y\in\left\{8;-8\right\}\end{matrix}\right.\)