
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 13:
$6-2\sqrt{5}=5-2\sqrt{5}.\sqrt{1}+1$
$=(\sqrt{5}-1)^2$
Tương tự: $6+2\sqrt{5}=(\sqrt{5}+1)^2$
Do đó:
$M=\sqrt{(\sqrt{5}+1)^2}-\sqrt{(\sqrt{5}-1)^2}$
$=|\sqrt{5}+1|-|\sqrt{5}-1|=(\sqrt{5}+1)-(\sqrt{5}-1)$
$=2$
Bài 14:
a.
$M=\sqrt{4+2\sqrt{4}.\sqrt{5}+5}-\sqrt{4-2\sqrt{4}.\sqrt{5}+5}$
$=\sqrt{(\sqrt{4}+\sqrt{5})^2}-\sqrt{(\sqrt{4}-\sqrt{5})^2}$
$=|\sqrt{4}+\sqrt{5}|-|\sqrt{4}-\sqrt{5}|$
$=2+\sqrt{5}-(\sqrt{5}-2)=4$
b.
$N=\sqrt{7-2\sqrt{7}+1}-\sqrt{7+2\sqrt{7}+1}$
$=\sqrt{(\sqrt{7}-1)^2}-\sqrt{(\sqrt{7}+1)^2}$
$=|\sqrt{7}-1|-|\sqrt{7}+1|$
$=(\sqrt{7}-1)-(\sqrt{7}+1)=-2$


Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)

Câu 23:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-x^2-x+2=0\\y=-x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(x-1\right)=0\\y=-x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(-2;-4\right);\left(1;-1\right)\right\}\)
c: Vì (d1)//(d) nên a=1
Vậy: (d1): y=x+b
Thay x=-1 và y=2 vào (d1), ta được:
b-1=2
hay b=3


1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)

Bài 3:
a: Gọi OK là khoảng cách từ O đến AB
Suy ra: K là trung điểm của AB
hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
hay OK=3(cm)
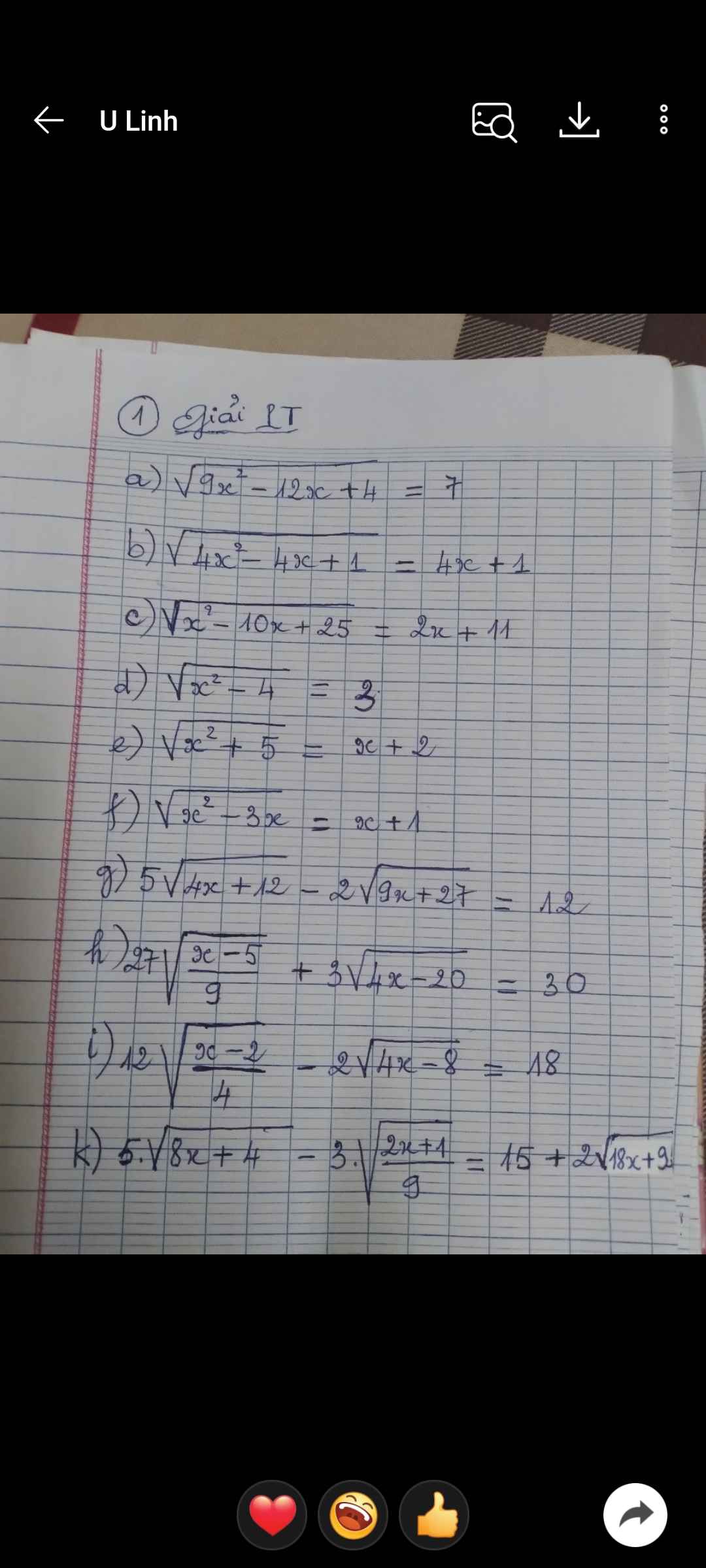







 , mình đang cần giải gấp. Cảm ơn mn nhiều.
, mình đang cần giải gấp. Cảm ơn mn nhiều.