
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt : \(\dfrac{x}{5}=\dfrac{y}{3}=k\)
`=>x=5k,y=3k`
Ta có : \(x^2-y^2=4=>\left(5k\right)^2-\left(3k\right)^2=4\\ =>25k^2-9k^2=4\\ =>16k^2=4\\ =>k^2=\dfrac{1}{4}\\ =>k=\pm\dfrac{1}{2}\)
\(=>\left[{}\begin{matrix}\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=\dfrac{3}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x=-\dfrac{5}{2}\\y=-\dfrac{3}{2}\end{matrix}\right.\end{matrix}\right.\)


Bài làm:
Gọi chiều dài và chiều rộng của hình chữ nhật đó lần lượt là x và y ( x>y>0 )
Vì chiều dài và chiều rộng của HCN đó tỉ lệ với 4 và 3 nên ta có:\(\frac{x}{4}=\frac{y}{3}\)
Ta đặt \(\frac{x}{4}=\frac{y}{3}=k\)( k>0 )
Suy ra: \(\hept{\begin{cases}x=4k\\y=3k\end{cases}}\)
Vậy chu vi hình chữ nhật đó là:
\(\left(4k+3k\right).2=14k\)( thỏa mãn)
Vậy chu vi hình chữ nhật đó là 14k.
Chúc bạn học tốt!

Bài 3:
Ta có: a//b
nên \(x+y=180\)
mà \(2x-3y=0\)
nên \(\left\{{}\begin{matrix}x+y=180\\2x-3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+2y=180\\2x-3y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5y=180\\x+y=180\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=36\\x=144\end{matrix}\right.\)

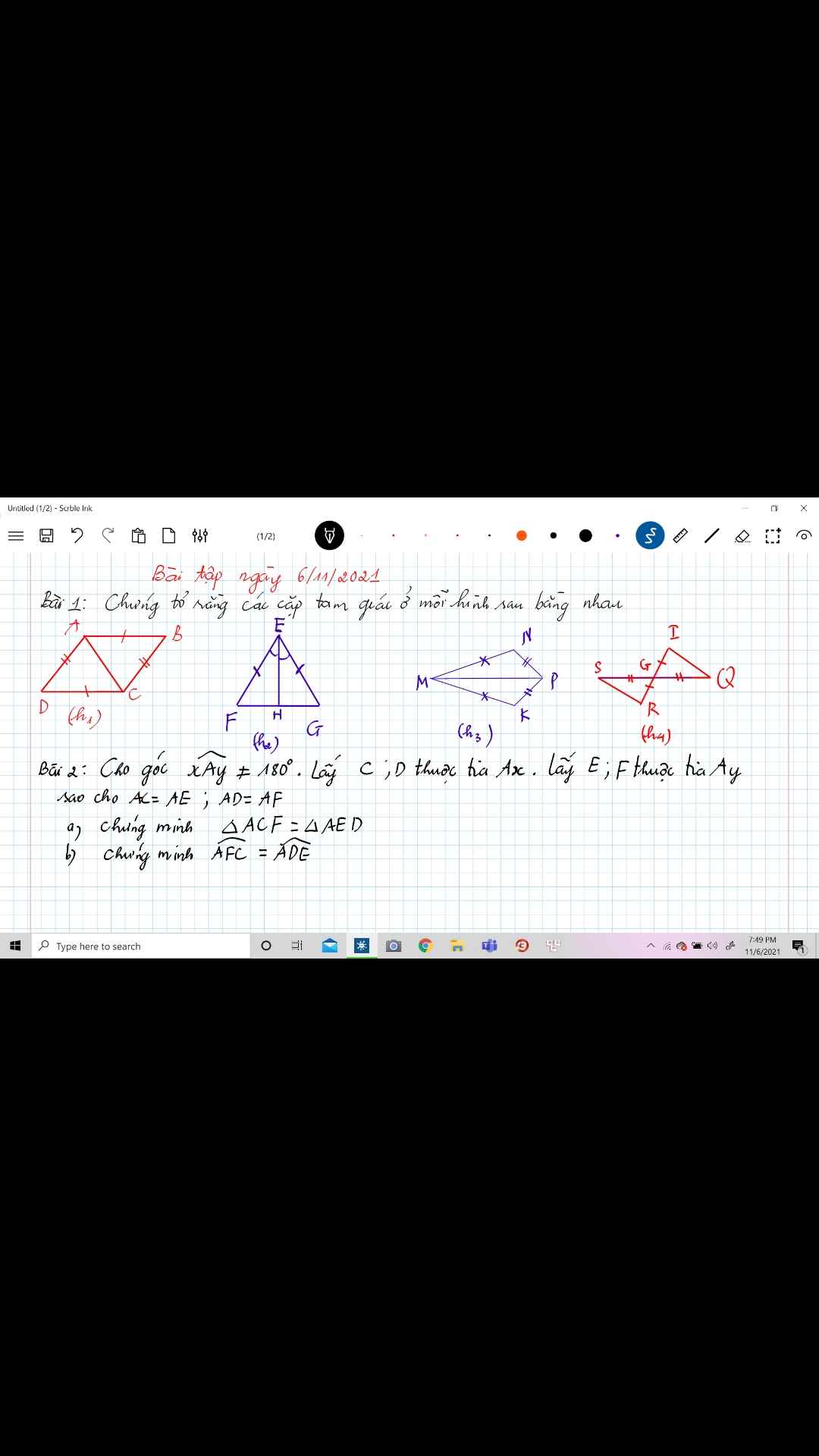
a: Xét ΔACF và ΔAED có
AC=AE
\(\widehat{A}\) chung
AF=AD
Do đó: ΔACF=ΔAED

bài 2
a)
\(=3\left(x-y\right)+5x\left(x-y\right)\)
\(=\left(3+5x\right)\left(x-y\right)\)
c)
\(=x\left(x-1\right)+y\left(x-1\right)=\left(x+y\right)\left(x-1\right)\)
d)
\(=7x\left(5x-y\right)+2\left(5x-y\right)+3y\left(5x-y\right)\)
\(=\left(7x+2+3y\right)\left(5x-y\right)\)
e)
=\(2y\left(3-x\right)-3xy\left(3-x\right)=\left(2-3x\right)\left[y\left(3-x\right)\right]\)
bài 1
a) = x(5x-6)
b) = 3x(y+4x)
c)=6x2(4x+1)
d)=\(2ab\left(a-2\right)\)
e)\(=\left(x-5y\right)\left(x+y\right)\)
f) \(\left(x-y\right)\left(y+2\right)\)

 Giúp Mik 2 bài này nha mik cảm ơn nhiều ạ
Giúp Mik 2 bài này nha mik cảm ơn nhiều ạ

bài ở đâu vậy bạn