
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


R=1/2CD=a
h=AD=2a
S1=Sxq=2*pi*r*h=2*pi*a*2a=4*pi*a^2
S2=Stp=2*pi*r^2+2*pi*r*h
=2*pi*a^2+2*pi*a*2a
=6*pi*a^2
>S1/S2=2/3

a: =>x=y+11
xy=60
=>y(y+11)=60
\(\Leftrightarrow y^2+15y-4y-60=0\)
=>(y+15)(y-4)=0
hay \(y\in\left\{-15;4\right\}\)


10: =>1/2x=3/4 và x+y=2
=>x=3/4*2=3/2 và y=1/2
11:=>4x+5y=3 và 4x-12y=20
=>17y=-17 và x-3y=5
=>y=-1 và x=3y+5=-3+5=2
12: =>7x-2y=1 và 6x+2y=12
=>13x=13 và 3x+y=6
=>x=1 và y=3
13:=>2/x=1 và 1/x-1/y=1/5
=>x=2 và 1/y=1/2-1/5=3/10
=>y=10/3 và x=2
14: =>12/x-16/y=8 và 12/x-15/y=9
=>-1/y=-1 và 4/x-5/y=3
=>y=1 và 4/x=3+5=8
=>x=1/2 và y=1

a: Khi m=3 thì (1): x^2-6x+4=0
=>x^2-6x+9-5=0
=>(x-3)^2=5
=>\(x=3\pm\sqrt{5}\)

a: Δ=(m-2)^2-4(m-4)
=m^2-4m+4-4m+16
=m^2-8m+20
=m^2-8m+16+4
=(m-2)^2+4>=4>0
=>Phương trình luôn có 2 nghiệm pb
b: x1^2+x2^2
=(x1+x2)^2-2x1x2
=(m-2)^2-2(m-4)
=m^2-4m+4-2m+8
=m^2-6m+12
=(m-3)^2+3>=3
Dấu = xảy ra khi m=3

a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2

\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}\)
=>\(2R^2-AB^2=2\cdot R^2\cdot\dfrac{\sqrt{3}}{2}=R^2\cdot\sqrt{3}\)
=>\(AB^2=R^2\cdot\left(2-\sqrt{3}\right)\)
=>\(AB=R\sqrt{2-\sqrt{3}}=\dfrac{R}{\sqrt{2}}\cdot\left(\sqrt{3}-1\right)\)
\(AC=\sqrt{R^2+R^2}=R\sqrt{2}\)
góc OBA=(180-30)/2=75 độ
góc BOC=90+30=120 độ
góc OCA=45 độ
=>góc BAC=360-120-75-45=240-120=120 độ
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(\dfrac{\dfrac{R^2}{2}\cdot\left(4-2\sqrt{3}\right)+2R^2-BC^2}{2\cdot\dfrac{R}{\sqrt{2}}\cdot\left(\sqrt{3}-1\right)\cdot R\sqrt{2}}=\dfrac{-1}{2}\)
=>\(R^2\left(2-\sqrt{3}\right)+2R^2-BC^2=-\dfrac{R}{\sqrt{2}}\cdot\left(\sqrt{3}-1\right)\cdot R\sqrt{2}\)
\(\Leftrightarrow R^2\left(4-\sqrt{3}\right)-BC^2=-2R^2\left(\sqrt{3}-1\right)\)
\(\Leftrightarrow R^2\left(4-\sqrt{3}+2\sqrt{3}-2\right)-BC^2=0\)
=>\(BC^2=R^2\cdot\left(2+\sqrt{3}\right)\)
=>\(BC=R\sqrt{2+\sqrt{3}}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot sin120\cdot\dfrac{R}{\sqrt{2}}\left(\sqrt{3}-1\right)\cdot R\sqrt{2}\)
\(=\dfrac{1}{2}\cdot R^2\cdot\dfrac{\sqrt{3}}{2}\cdot\left(\sqrt{3}-1\right)=R^2\cdot\dfrac{3-\sqrt{3}}{4}\)

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
=>ΔAMB vuông tại M
=>AM vuông góc MB
=>AM vuông góc DC tại K
M là điểm chính giữa của cung AC
nên MA=MC
mà OA=OC
nen OM là trung trực của AC
=>OM vuông góc AC
Xét tứ giác CHMK có
góc CHM+góc CKM=180 độ
=>CHMK là tứ giác nội tiếp
b: Xét tứ giác DMBC có
DC//BM
DM//CB
=>DMBC là hình bình hành
=>DC=MB; DM=BC


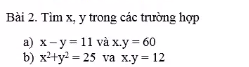

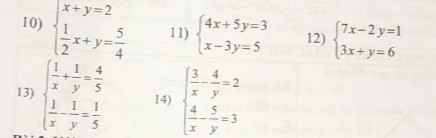


 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ


\(S_{Xq}=2\cdot pi\cdot2^2+\dfrac{1}{2}\cdot\sqrt{5}\cdot2=3\sqrt{5}\cdot pi\)