
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chia mỗi quả táo ra 9 phần, mỗi người một phần của quả táo.
Như vậy, mỗi người được 8 phần.
@Cỏ
#Forever

a. \(f\left(x\right)_{max}=f\left(-2\right)=111\) ; \(f\left(x\right)_{min}=f\left(1\right)=-6\)
b. \(f\left(x\right)_{max}=f\left(-3\right)=7\) ; \(f\left(x\right)_{min}=f\left(0\right)=1\)
c. \(f\left(x\right)_{max}=f\left(4\right)=\dfrac{2}{3}\) ; \(f\left(x\right)_{min}\) ko tồn tại
d.
Miền xác định: \(D=\left[-2\sqrt{2};2\sqrt{2}\right]\)
\(y'=\dfrac{2\left(4-x^2\right)}{\sqrt{8-x^2}}=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
\(f\left(-2\sqrt{2}\right)=f\left(2\sqrt{2}\right)=0\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=4\)
\(f\left(x\right)_{max}=f\left(2\right)=4\) ; \(f\left(x\right)_{min}=f\left(-2\right)=-4\)


a. Để hàm số đã cho có một cực trị thì -m(2m-1)>0 \(\Rightarrow\) 0<m<1/2.
b. Để hàm số đã cho có ba cực trị thì -m(2m-1)<0 \(\Rightarrow\) m<0 hoặc m>1/2.
c. Để hàm số đã cho có một cực trị là cực đại thì m<0 và -(2m-1)<0, suy ra không có giá trị nào của m thỏa yêu cầu của bài toán.


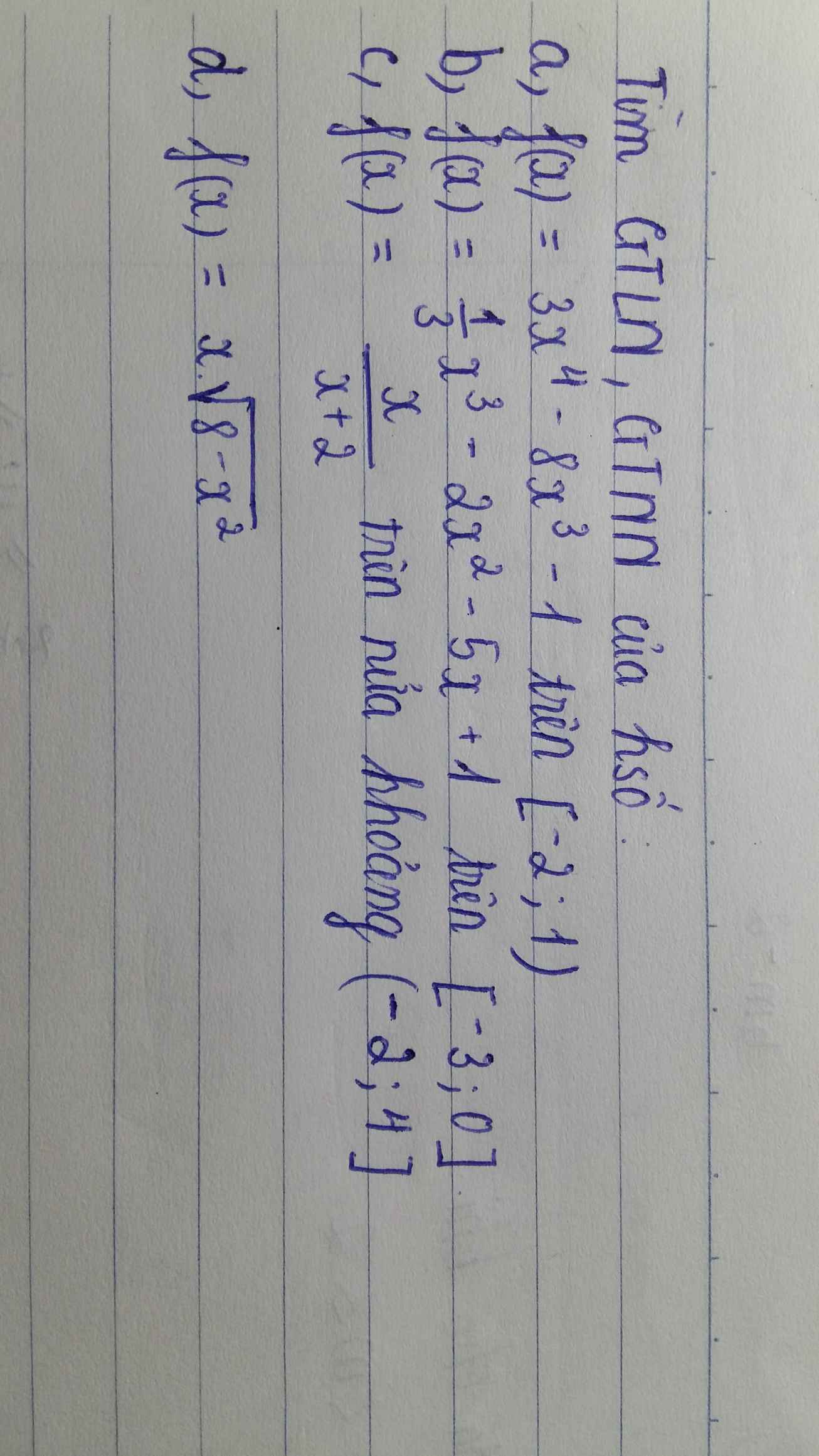

Cắt mỗi quả thành 8 phần bằng nhau, như vậy 7 quả sẽ được 56 phần. Sau đó chia đều cho 8 người, mỗi người được 7 phần như nhau.
7 quả táo chia cho mỗi người thì mỗi người đc 7/8 số táo
chia mỗi quả táo thành 8 miếng
Suy ra mỗi người 7 miếng