XB
hú ý phần bài a và b đã chứng minh hết rùi nhen
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
2
S
1 tháng 7 2018
Đặt a/b=c/d=k => a=bk,c=dk
Ta có: \(\frac{a}{b}=\frac{bk}{b}=k\left(1\right)\)
\(\frac{7a+5c}{7b+5d}=\frac{7bk+5dk}{7b+5d}=\frac{k\left(7b+5d\right)}{7b+5d}=k\left(2\right)\)
Từ (1) vavf (2) => a/b=7a+5c/7b+5d
TR
4 tháng 6 2018
Mik cũng mún giúp bạn lắm nhưng mà mik kém toán ( mik suy nghĩ rồi mà nó ko ra dc chữ nào bạn ạ)
Khi nào bạn hỏi về môn Văn hoặc Anh thì mik sẽ giúp bạn...
QUYỂN NÀY NÈ
21 tháng 9 2016
1/ Ta có \(\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}\)
\(\Leftrightarrow\frac{abz-acy}{a^2}=\frac{bcx-abz}{b^2}=\frac{acy-bcx}{c^2}=\frac{abz-acy+bcx-abz+acy-bcx}{a^2+b^2+c^2}=0\)
\(\Rightarrow bz-cy=cx-az=ay-bx=0\Leftrightarrow\frac{x}{a}=\frac{y}{b}=\frac{z}{c}\)
2/ Giả sử \(a>b\Rightarrow\frac{a}{b}>1\)
Ta sẽ chứng minh \(\frac{a}{b}>\frac{a+2017}{b+2017}\) . Thật vậy : \(\frac{a}{b}>\frac{a+2017}{b+2017}\Leftrightarrow ab+2017a>ab+2017b\Leftrightarrow a>b\) luôn đúng
Giả sử \(a< b\) thì \(\frac{a}{b}< 1\Rightarrow\frac{a}{b}< \frac{a+2017}{b+2017}\) . Thật vậy :
\(\frac{a}{b}< \frac{a+2017}{b+2017}\Rightarrow ab+2017a< ab+2017b\Leftrightarrow a< b\) luôn đúng
Giả sử \(a=b\Leftrightarrow\frac{a}{b}=1=\frac{2017}{2017}=\frac{a+2017}{b+2017}\)
TT
6 tháng 5 2021
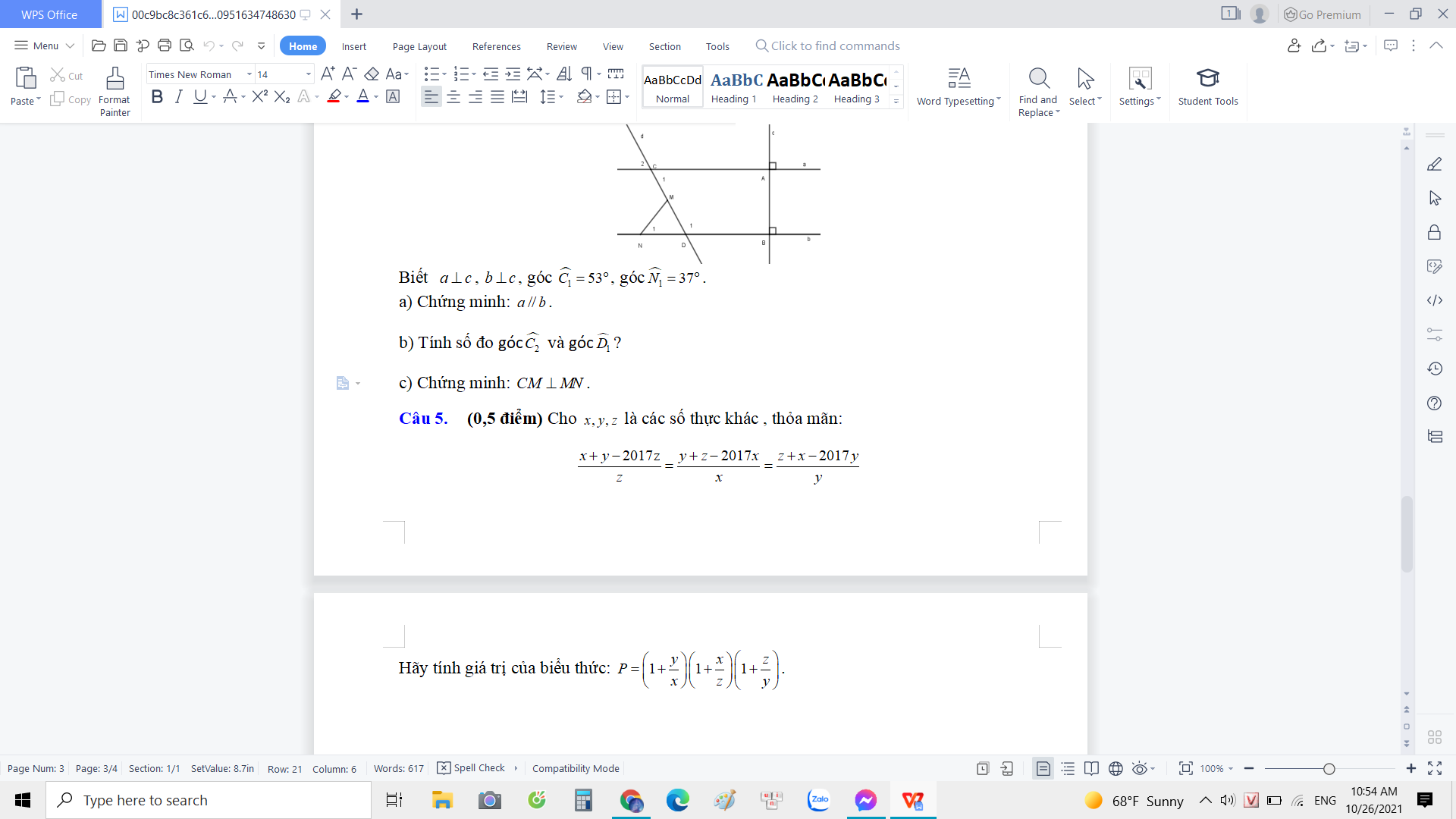
hình bạn tự vẽ nhé
a. ví tam giác ABC là tam giác cân và có góc A bằng 90 độ nên tam giác ABC là tam giác vuông cân tại A
=> góc BAC = 90 độ và AB=AC
Xét tứ giác ABIC có góc BAC =90 độ, góc ABI = 90 độ (vì AIvuông góc với AB ), góc ACI =90độ (vì AC vuông góc với CI)
=> tứ giác ABIC là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
mà AB=AC (cmt)
=> Tứ giác ABIC là hình vuông (dấu hiệu nhận biết hình vuông)
=> AI là phân giác góc BAC
LC
26 tháng 8 2015
\(\frac{4^6.9^5+6^9.120}{8^4.3^{12}-6^{11}}=\frac{\left(2^2\right)^6.\left(3^2\right)^5+\left(2.3\right)^9.2^3.3.5}{\left(2^3\right)^4.3^{12}-\left(2.3\right)^{11}}=\frac{2^{12}.3^{10}+2^9.3^9.2^3.3.5}{2^{12}.3^{12}-2^{11}.3^{11}}\)
\(=\frac{2^{12}.3^{10}+2^{12}.3^{10}.5}{2^{12}.3^{12}-2^{11}.3^{11}}=\frac{2^{12}.3^{10}.\left(1+5\right)}{6^{12}-6^{11}}=\frac{2^{12}.3^{10}.6}{6^{11}.\left(6-1\right)}=\frac{2^{12}.3^{10}.2.3}{6^{11}.\left(6-1\right)}=\frac{2^{13}.3^{11}}{6^{11}.5}=\frac{2^{11}.3^{11}.2^2}{6^{11}.5}=\frac{6^{11}.4}{6^{11}.5}=\frac{4}{5}\)
26 tháng 8 2015
Bài2
a) ta có : 10^19 + 10^18 +10^17 = 10^17 (10^2+10+1)
= 10^17 . 111
Do 10 chia hết cho 5 nên 10^17 cũng chia hết cho 5. Mà 10^17 cũng chia hết cho 111
nên 10^17 chia hết cho 111x5 = 555 ( vì (111;5)=1)
Vậy 10^19 + 10^18 + 10^17 chia hết cho 555
b) Ta có : 7+7^2+7^3+7^4+...+7^84
= (7+7^2+7^3)+(7^4+7^5+7^6)+...+(7^82+7^83+7^84)
= 7(1+7+7^2) + 7^4(1+7+7^2)+...+7^82(1+7+7^2)
= 7.57 + 7^4.57 +...+ 7^82.57
= 57(7.7^4....7^82) chia hết cho 57
Vậy 7+7^2+7^3+...+7^84 chia hết cho 57
NT
0
