Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

thứ 1: Thầy cô ko hiểu
thứ 2: những từ viết tắt có thể bị hiểu sai nghĩa hoặc những từ đó ko cho phép viết tắt
=> không nên viết tắt
![]()

a.
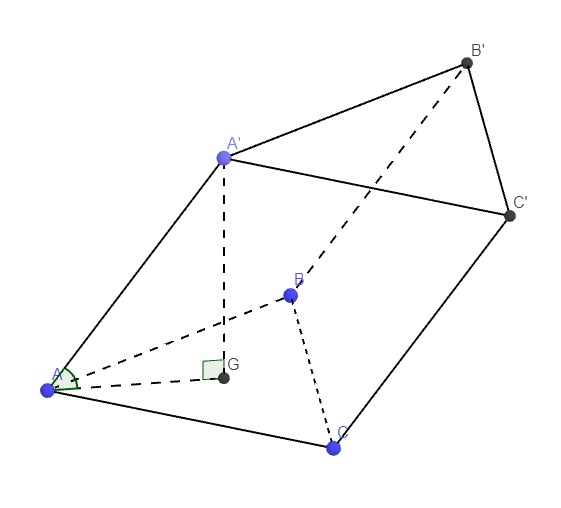
Do A' cách đều A,B,C \(\Rightarrow A'A=A'B=A'C\) hay \(A'ABC\) là chóp tam giác đều
\(\Rightarrow\) Hình chiếu vuông góc của A' lên (ABC) trùng trọng tâm ABC
Gọi G là trọng tâm ABC \(\Rightarrow A'G\perp\left(ABC\right)\)
\(\Rightarrow A'G\) là đường cao lăng trụ
Lại có \(A'G\perp\left(ABC\right)\Rightarrow AG\) là hình chiếu vuông góc của A'A lên (ABC)
\(\Rightarrow\widehat{A'AG}\) là góc giữa A'A và (ABC) \(\Rightarrow\widehat{A'AG}=60^0\)
\(AG=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow A'G=AG.tan60^0=a\)
b.
Đề bài thật kì quặc, ở giả thiết đã cho sẵn góc giữa A'A và (ABC) là 60 độ sao còn bắt tính?
Còn góc đó chúng ta đã xác định ở câu a là \(\widehat{A'AG}\)


Chọn $k$ đồ vật cùng lúc trong $n$ đồ vật thì chọn A.
Chọn $k$ đồ vật lần lượt thì sẽ chọn đáp án B như bạn nói. Lý giải:
Chọn lần 1, có $n$ cách chọn
Chọn lần 2, có $n-1$ cách chọn
.....
Chọn lần $k$, có $n-k+1$ cách chọn
Số cách chọn: $n(n-1)...(n-k+1)=\frac{n!}{(n-k)!}=A^k_n$

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

Đáp án C
Số cách đi từ A đến B là 4, số cách đi từ B đến C là 2
số cách đi từ C đến D là 3.
Số cách đi từ A đến D mà qua B và C chỉ một lần là:
4.2.3 = 24(cách)

Từ A đến B có 4 cách.
Từ B đến C có 2 cách.
Từ C đến D có 2 cách.
Vậy theo qui tắc nhân ta có 4.2.3 = 24 cách.
Chọn đáp án D.