Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số f x = ln x + 1 + x 2
là một nguyên hàm của g x = 1 1 + x 2

a) Hàm số 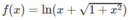
là một nguyên hàm của 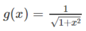
b) Hàm số g(x) = esinx là một nguyên hàm của hàm số f(x) = esinx.cosx
c) Hàm số 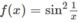
là một nguyên hàm của hàm số 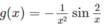

Hàm số g x = e sinx là một nguyên hàm của hàm số f x = e sinx cosx

Chọn A.
F ' ( x ) = sin x - cos x ' sin x - cos x = cos x + sin x sin x - cos x

Để kiểm tra một hàm F(x) có phải là một nguyên hàm của f(x) không thì ta chỉ cần kiểm tra F'(x) có bằng f(x) không?
a) \(F\left(x\right)\) là hằng số nên \(F'\left(x\right)=0\ne f\left(x\right)\)
b) \(G'\left(x\right)=2.\dfrac{1}{2}.\dfrac{1}{\cos^2x}=1+\tan^2x\)
c) \(H'\left(x\right)=\dfrac{\cos x}{1+\sin x}\)
d) \(K'\left(x\right)=-2.\dfrac{-\left(\dfrac{1}{2}.\dfrac{1}{\cos^2\dfrac{x}{2}}\right)}{\left(1+\tan\dfrac{x}{2}\right)^2}=\dfrac{\dfrac{1}{\cos^2\dfrac{x}{2}}}{\left(\dfrac{\cos\dfrac{x}{2}+\sin\dfrac{x}{2}}{\cos\dfrac{x}{2}}\right)^2}\)
\(=\dfrac{1}{\left(\cos\dfrac{x}{2}+\sin\dfrac{x}{2}\right)^2}=\dfrac{1}{1+2\cos\dfrac{x}{2}\sin\dfrac{x}{2}}\)
\(=\dfrac{1}{1+\sin x}\)
Vậy hàm số K(x) là một nguyên hàm của f(x).
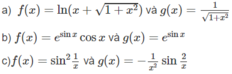


Hàm số f x = sin 2 1 x
là một nguyên hàm của hàm số g x = - 1 x 2 sin 2 x