Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Để phá vỡ hạt nhân này thành các nuclôn riêng lẻ, cần một công đúng bằng một lực liên kết của hạt nhân.
W l k = ∆ m c 2 = ( Z m p + ( A - Z ) m n - m N i ) c 2 = 105 , 0732 ( M e V )

\(\alpha + _7^{14}N \rightarrow _1^1p + _8^{17}O\)
\(m_t-m_s = m_{\alpha}+m_N - (m_{O}+m_p) =- 1,3.10^{-3}u < 0\), phản ứng thu năng lượng.
\(W_{thu} = (m_s-m_t)c^2 = K_t-K_s\)
=> \(1,3.10^{-3}.931,5 = K_{He}+K_N- (K_p+K_O)\)(do Nito đứng yên nên KN = 0)
=> \(K_p +K_O = 6,48905MeV. (1)\)
Áp dụng định luật bảo toàn động lượng
\(\overrightarrow P_{\alpha} =\overrightarrow P_{p} + \overrightarrow P_{O} \)
Dựa vào hình vẽ ta có (định lí Pi-ta-go)
\(P_{O}^2 = P_{\alpha}^2+P_p^2\)
=> \(2m_{O}K_{O} = 2m_{He}K_{He}+ 2m_pK_p.(2)\)
Từ (1) và (2) giải hệ phương trình ta được
\(K_p = 4,414MeV; K_O = 2,075 MeV.\)

- Năng lượng tối thiểu để phân chia hạt nhân 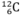 thành ba hạt α là :
thành ba hạt α là :
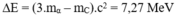

\(_1^1p + _4^9Be \rightarrow _2^4He + _3^6X\)
Áp dụng định luật bảo toàn động lượng \(\overrightarrow P_p=\overrightarrow P_{He}+ \overrightarrow P_{X} \) (do hạt Be đứng yên)
Dựa vào hình vẽ ta có \(P_{p}^2+ P_{He}^2 = P_X^2\)
=> \(2m_{p}K_{p}+2m_{He} K_{He} = 2m_{X}K_{X}. \)
=> \(K_{p}+4K_{He} = 6K_{X} => K_X = 6MeV.\)

Độ dôi khối của các hạt nhân sau phản ứng tổng hợp hạt nhân :
m p + m n - m α + m A l = (29,970 + 1,0087) u - (4,0015 + 26,974) u = 0,0032 u
Động năng tối thiểu của hạt α để phản ứng này có thể xảy ra :
W đ α m i n = 931.0,0032 ≈ 2,98 MeV

- Năng lượng liên kết của từng hạt trong phản ứng là:
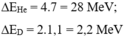
- Năng lượng tỏa ra là:
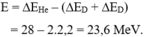
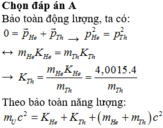
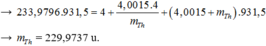

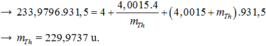
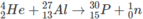

Đáp án B
Để phá vỡ hạt nhân này thành các nuclôn riêng lẻ, cần một công đúng bằng một lực liên kết của hạt nhân:
W l k = ∆ m c 2 = ( Z m p + ( A - Z ) m n - m N i ) c 2