Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: 27km/h27km/h
Giải thích các bước giải:
Gọi vận tốc riêng của cano là x,x>3x,x>3
→→Vận tốc cano khi xuôi dòng là x+3,x+3, khi ngược dòng là x−3x−3
Thời gian cano đi hết quãng đường từ A đến B và trở về là:
10h36′−6h30′=4h6′=4110(h)10h36′−6h30′=4h6′=4110(h)
Do cano đi hết quãng đường AB, nghỉ 30′=12h30′=12h, và trở về từ B về A
→48x+3+12+48x−3=4110→48x+3+12+48x−3=4110
→x=27→x=27 vì x>3

Gọi khoảng cách giữa AB là x(km).
Thời gian cano đi xuôi là: x/30(h)
Vận tốc cano ngược dòng là 20km
Vậy thời gian di ngược là x/20(h)
Thời gian xuôi ít hơn tg ngược 1h20'=4/3h nên ta có pt x/30+4/3=x/20
x = 80

Gọi x (km/h) là vận tốc thực của ca nô. Điều kiện: x > 6
Vận tốc của ca nô khi xuôi dòng là x + 6 (km/h)
Vận tốc của ca nô khi ngược dòng là x – 6 (km/h)
Thời gian lúc ca nô đi xuôi dòng là 36/(x + 6) (giờ)
Thời gian lúc ca nô đi ngược dòng là 36/(x - 6) (giờ)
Thời gian ca nô đi và về:
11 giờ 30 phút – 7 giờ = 4 giờ 30 phút = 9/2 giờ
Theo đề bài, ta có phương trình:
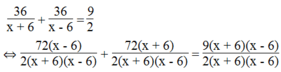
⇔ 72(x – 6) + 72(x + 6) = 9(x + 6)(x – 6)
⇔ 72x – 432 + 72x + 432 = 9x2 – 324
⇔ 9x2 – 144x – 324 = 0
⇔ x2 – 16x – 36 = 0
⇔ x2 + 2x – 18x – 36 = 0
⇔ x(x + 2) – 18(x + 2) = 0
⇔ (x + 2)(x – 18) = 0
⇔ x + 2 = 0 hoặc x – 18 = 0
x + 2 = 0 ⇔ x = -2 (loại)
x – 18 = 0 ⇔ x = 18 (thỏa)
Vậy vận tốc thực của ca nô là 18km/h, suy ra vận tốc của ca nô lúc xuôi dòng là 18 + 6 = 24 (km/h).

Lời giải:
Gọi vận tốc cano lúc yên lặng là $x$ km/h thì vận tốc xuôi dòng là $x+3$ km/h và vận tốc xuôi dòng là $x-3$ km/h
Tổng thời gian đi lẫn về là:
$\frac{60}{x+3}+\frac{60}{x-3}=11h-7h=4$ (h)
Giải pt trên với điều kiện $x>3$ ta suy ra $x\approx 30,3$ (km/h)