Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kết quả tính độ dãn dài tỉ đối của thanh thép ở những nhiệt độ t khác nhau (được ghi ở bảng bên)
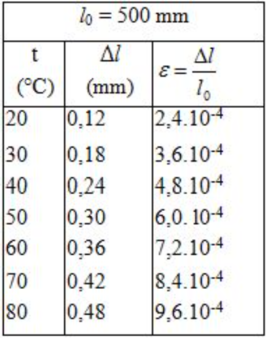

Hình 36.1G có dạng đoạn thẳng.
Điều này chứng tỏ độ biến dạng tỉ đối ∆ l/ l 0 của thanh sắt tỉ lệ thuận với độ tăng nhiệt độ t (tính từ 0 ° C):
∆ l/ l 0 = α t
Nhận xét thấy hệ số tỉ lệ α chính là hệ số nở dài của thép.
Hệ số tỉ lệ α được xác định bởi hệ số góc của đường biểu diễn đồ thị ở Hình 36.1G.

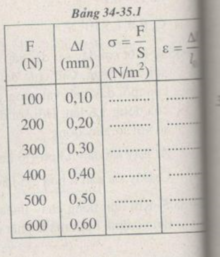
Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào σ
Chọn tỉ lệ vẽ trên các trục tọa độ:
- Trục hoành: 1 cm → σ = 0,5. 10 8 N/ m 2
- Trục tung: 1 cm → ε = 0,2. 10 - 3
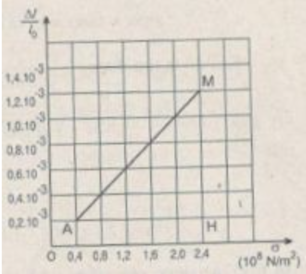
Đồ thị có dạng đường thẳng chứng tỏ độ biến dạng tỉ đối Δl/l0 của thanh sắt tỉ lệ thuận với ứng suất σ của lực kéo tác dụng lên thanh sắt, nghĩa là:
ε = ∆ l/ l 0 = a ε
Hệ số tỉ lệ a được xác định bởi hệ số góc của đường biểu diễn đồ thị:
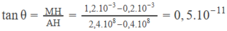

Khi nhiệt độ tăng từ 0 ° C đến t ° C thì độ dãn dài của :
- Thanh thép : ∆ l 1 = l 01 α 1 t.
- Thanh đồng : ∆ l 2 = l 02 α 2 t.
Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t ° C có giá trị bằng :
∆ l = ∆ l 1 - l 2 l 1 = l 01 α 1 t - l 02 α 2 t = ( l 01 α 1 - l 02 α 2 )t = 25 mm
Công thức này chứng tỏ ∆ l phụ thuộc bậc nhất vào t.
Rõ ràng, muốn ∆ l không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :
l 01 α 1 - l 02 α 2 = 0 ⇒ l 02 / l 01 = α 1 / α 2
hay:
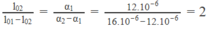
Từ đó suy ra độ dài ở 0 ° C của :
- Thanh đồng : l 02 = 2( l 01 - l 02 ) = ∆ l = 2.25 = 50 mm.
- Thanh thép : l 01 = l 02 + ∆ l = 50 + 25 = 75 mm.

Khi nhiệt độ tăng từ 0 ° C đến t ° C thì độ dãn dài của :
- Thanh thép : ∆ l 1 = l 01 α 1 t.
- Thanh đồng : ∆ l 2 = l 02 α 2 t.
Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t ° C có giá trị bằng :
∆ l = ∆ l1 – ∆ l2 = l 01 α 1 t – l 02 α 2 t = ( l 01 α 1 – l 02 α 1 )t = 50 mm
Công thức này chứng tỏ ∆ l phụ thuộc bậc nhất vào t. Rõ ràng, muốn ∆ l không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :
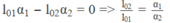
hay:
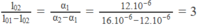
Từ đó suy ra độ dài ở 0 ° C của :
- Thanh đồng : l 02 = 3( l 01 - l 02 ) = ∆ l = 3.50 = 150 mm.
- Thanh thép : l 01 = l 02 + ∆ l = 150 + 50 = 200 mm.

Vì các thanh ray được đặt nối tiếp nhau, ở cả hai đầu thanh ray đều có khe hở và các thanh ray nở cả về hai đầu nên khe hở phải có độ rộng h tương ứng với độ nở dài của một thanh ray khi nhiệt độ tăng từ 25 ° C lên 60 ° C Áp dụng công thức: 1 = 1 0 ( 1 + α t )
![]()
![]()
![]()
![]()

![]()

a/ Chiều dài của thanh: \(l=l_0(1+\alpha.\Delta t)\)
Thanh nhôm: \(l=50.[1+24.10^{-6}.(170-20)]=50,18cm\)
Thanh thép: \(l=50,12.[1+12.10^{-6}.(170-20)]=50,21cm\)
b/ Giả sử ở nhiệt độ t, hai thanh có cùng chiều dài
\(\Rightarrow 50.[1+24.10^{-6}.(t-20)]=50,12.[1+12.10^{-6}.(t-20)]\)
Bạn giải phương trình trên rồi tìm t nhé ![]()
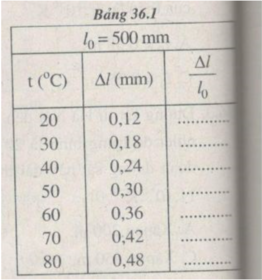
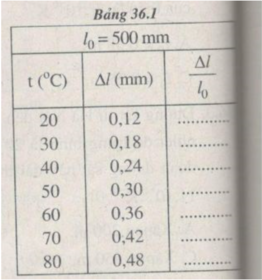
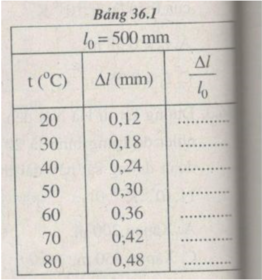

Chọn tỉ xích trên các trục toạ độ :
Trục hoành : 1 cm → t = 10 ° C.
Trục tung : 1 cm → = 1,2. 10 - 4
Đường biểu diễn đồ thị vẽ được trên