Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khảo sát hàm số 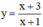
- TXĐ: D = R \ {-1}
- Sự biến thiên:
+ Chiều biến thiên:
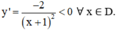
⇒ Hàm số nghịch biến trên các khoảng (-∞; -1) và (-1; +∞).
+ Cực trị: Hàm số không có cực trị.
+ Tiệm cận:
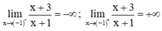
⇒ x = -1 là tiệm cận đứng của đồ thị hàm số.
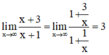
⇒ y = 3 là tiệm cận đứng của đồ thị hàm số.
+ Bảng biến thiên:
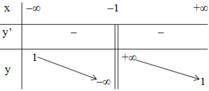
- Đồ thị:
+ Giao với Ox: (-3; 0)
+ Giao với Oy: (0; 3)
+ Đồ thị hàm số nhận (-1; 1) là tâm đối xứng.

a)
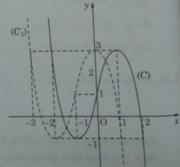
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
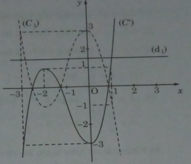
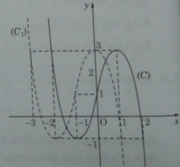
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
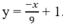
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔ 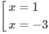
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.

a) Học sinh tự giải
b) 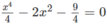
⇔ x 4 − 8 x 2 − 9 = 0
⇔ ( x 2 + 1)( x 2 − 9) = 0
⇔ 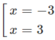
(C) cắt trục Ox tại x = -3 và x = 3
Ta có: y′ = x 3 − 4x
Phương trình tiếp tuyến của (C) tại điểm có hoành độ x = 3 và x = -3 lần lượt là:
y = y′(3)(x – 3) và y = y′(−3)(x + 3)
Hay y = 15(x – 3) và y = −15(x + 3)
c) 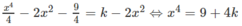
Từ đó, ta có:
k = −9/4: (C) và (P) có một điểm chung là (0; −9/4)
k > −9/4: (C) và (P) có hai giao điểm.
k < −9/4: (C) và (P) không cắt nhau.

Với a = 0 ta có hàm số 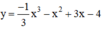
- Tập xác định : D = R.
- Sự biến thiên :
y’ = -x2 – 2x + 3 ;
y’ = 0 ⇔ x = -3 hoặc x = 1.
QUẢNG CÁOBảng biến thiên :
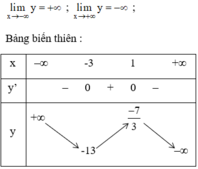
Kết luận :
Hàm số đồng biến trên (-3 ; 1)
Hàm số nghịch biến trên (-∞; -3) và (1; +∞).
Hàm số đạt cực đại tại x = 1 ; 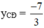
Hàm số đạt cực tiểu tại x = -3 ; yCT = -13.
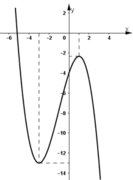
- Đồ thị hàm số :

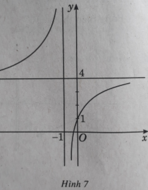
Với m = 0, hàm số trở thành: 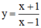
- TXĐ: D = R \ {1}
- Sự biến thiên:
+ Chiều biến thiên:
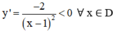
⇒ Hàm số nghịch biến trên (-∞; 1) và (1; +∞).
+ Cực trị: Hàm số không có cực trị.
QUẢNG CÁO+ Tiệm cận:
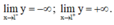
⇒ x = 1 là tiệm cận đứng của đồ thị hàm số.
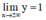
⇒ y = 1 là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên:
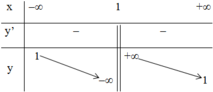
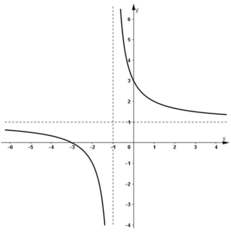
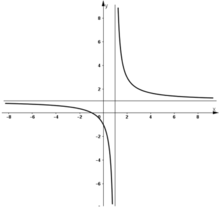
- Đồ thị:
+ Giao điểm với Ox: (-1; 0)
+ Giao điểm với Oy: (0; -1)

a) Học sinh tự làm
b) Ta có: y′ = –4 x 3 – 2x
Vì tiếp tuyến vuông góc với đường thẳng y = x/6 – 1 nên tiếp tuyến có hệ số góc là –6. Vì vậy:
–4 x 3 – 2x = –6
⇔ 2 x 3 + x – 3 = 0
⇔ 2( x 3 – 1) + (x – 1) = 0
⇔ (x – 1)(2 x 2 + 2x + 3) = 0
⇔ x = 1(2 x 2 + 2x + 3 > 0, ∀x)
Ta có: y(1) = 4
Phương trình phải tìm là: y – 4 = -6(x – 1) ⇔ y = -6x + 10

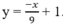
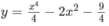
30% hi hi gu người
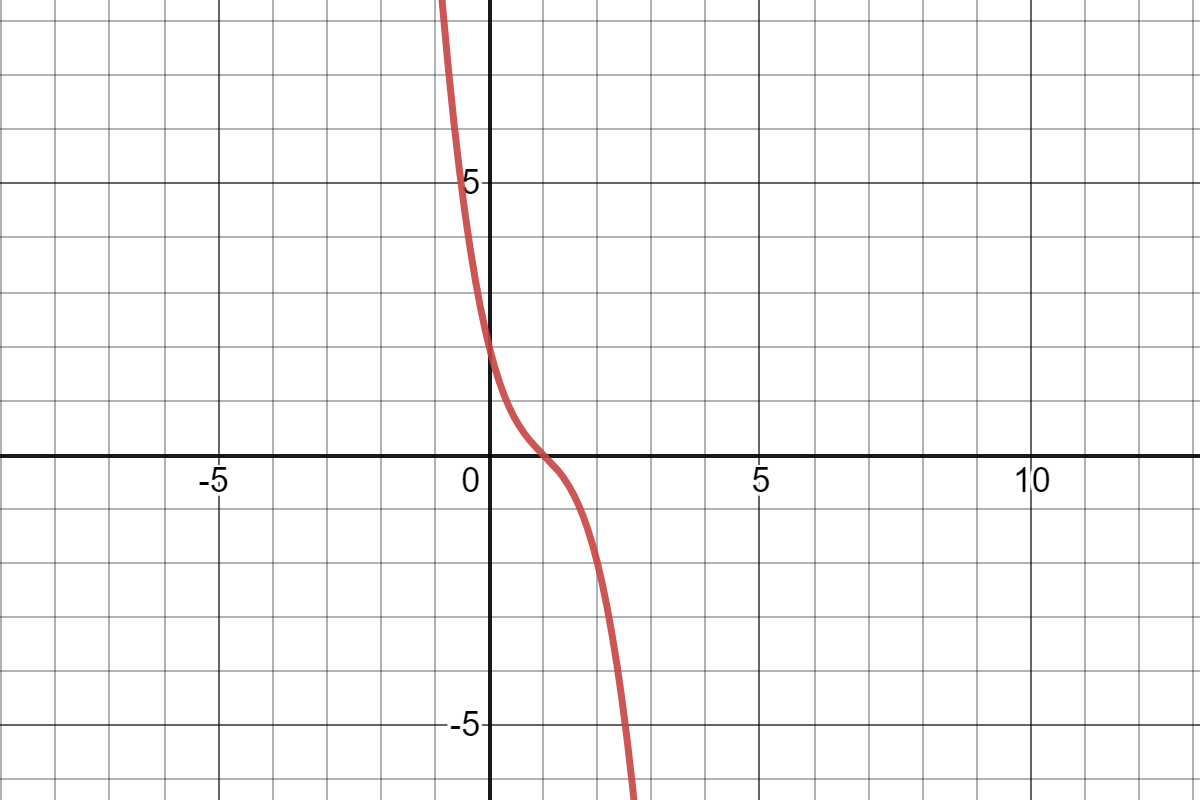
TXĐ :D=R
Ta có :\(lim_{x\rightarrow+\infty}\)=lim (-x3 +3x-1 )=+∞
\(lim_{x\rightarrow-\infty}\) =lim (-x3 +3x-1 ) =+∞
-> đồ thị hàm số ko có tiệm cận
lại có : y' =-3x2+x
y' =0 -> \(\left[\begin{array}{nghiempt}x=0\\x=\frac{1}{3}\end{array}\right.\)
bbt