Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


GIẢI :
Ta có : \(1+\frac{1}{100}=\frac{100}{100}+\frac{1}{100}=\frac{101}{100}\)
Vậy đáp án đúng nhất là đáp án C
_HT_

\(1+11+111+...+1111...1\)
=\(1+\left(1+10\right)+\left(1+10+100\right)+...+\left(1+10+100+...+100...0\right)\)
=\(\left(1+1+...+1\right)+\left(10+10+...+10\right)+...+100...0\)
=\(10+90+800+...+100...0\)
=\(1234567900\)
tham khảo
* Công thức: Nếu số hạng là các chữ số n và có m số hạng:
n x [m x 100 + (m - 1) x 101 + (m - 2) x102 + ………. +2 x 10m-2 + 1 x 10m-1]
(Bạn nhớ công thức giùm mình đi)
Ta có:
A = 1 + 11 + 111 + 1111 + ... + 1111111111
A = 1 (10.1 + 9.10 + 8.100 + 7.1000 + ... + 1.1000000000)
A = 1 (10 + 90 + 800 + 7000 + 60000 + 500000 + 4000000 + 30000000 + 200000000 + 1000000000)
A = 1 . 1234567900 = 1234567900

\(0+1+2+3+...+1000\)
\(=\frac{1001\left(1000+0\right)}{2}\)
\(=500500\)
\(0+1+2+3+4+5+...+1000\)
Số số hạng của dãy là : \((1000-0):1+1=1001\)số
Tổng của phép tính là : \(\frac{(1000+0)\cdot1001}{2}=500500\)
Chúc bạn hok tốt :>
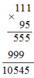
101 001
Đáp án D