Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Gọi A là biến cố “Đội tuyển Việt Nam và đội tuyển Malaysia được xếp trong cùng một bảng”.
Ta có: ![]() .
.
Do đó: 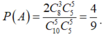 .
.

Đáp án : C
Để chọn một nam và một nữ đi dự trại hè, ta có:
Có 6 cách chọn học sinh khối 12.
Có 3 cách chọn học sinh khối 11.
Có 6 cách chọn học sinh khối 10.
Vậy theo qui tắc nhân ta có 6.3.6=108 cách.

Chọn C
Số phần tử của không gian mẫu là: ![]() .
.
Gọi biến cố A: “ Hai người được chọn đều là nam”.
![]()
Vậy xác suất cần tìm là: 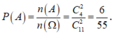 .
.

Gọi số học sinh nam là x \(\Rightarrow\) nữ là \(30-x\) (\(2\le x< 30\))
Không gian mẫu: \(C_{30}^3\)
Số cách chọn ra 2 nam và 1 nữ: \(C_x^2.C_{30-x}^1\)
Xác suất: \(\frac{C_x^2C_{30-x}^1}{C_{30}^3}=\frac{12}{29}\)
\(\Rightarrow x=16\)
Vậy có 16 nam và 14 nữ

Gọi A là biến cố: “có ít nhất một viên trúng vòng 10.”
⇒ A ¯ là biến cố: “Không viên nào trúng vòng 10.”
Gọi X là biến cố người thứ 1 bắn trúng vào10: P ( X ) = 0 , 75 ; P ( X ¯ ) = 1 − 0 , 75 = 0 , 25
Gọi Y là biến cố người thứ 2 bắn trúng vào10: P ( Y ) = 0 , 85 ; P ( Y ¯ ) = 1 − 0 , 85 = 0 , 15
Ta có; A ¯ = X ¯ . Y ¯ ; hai biến cố X ¯ ; Y ¯ là hai biến cố độc lập với nhau nên ta có:
P ( A ¯ ) = P ( X ¯ ) . P ( Y ¯ ) = 0 , 25. 0 , 15 = 0 , 0375
Do đó, xác suất của biến cố A là:
P ( A ) = 1 − P ( A ¯ ) = 1 − 0 , 0375 = 0 , 9625
Chọn đáp án A.

Đáp án C
Để đạt được 6 điểm thì thí sinh đó phải trả lời đúng 30 câu và trả lời sai 20 câu.
Xác suất trả lời đúng trong 1 câu là 0,25. Xác suất trả lời sai trong 1 câu là 0,75.
Vậy xác suất cần tìm là
![]()

Xác suất để rút ra cả 2 quả đều ko ghi số 12:
\(\dfrac{11}{12}.\dfrac{11}{12}=\dfrac{121}{144}\)
Xác suất thỏa mãn: \(1-\dfrac{121}{144}=\dfrac{23}{144}\)

có 18 số cần tìm.
gọi số cần tìm là abc
xét a=1, c có 3 cách chọn(0,2,8), b có 4 cách => có 3*4=12
xét abc<270, a=2, nếu c=8 thì b có 3 cách, nếu c=0 thì b có 2 cách => có 1*1*3+1*1*2=6
xét 270 đến 278, ko có số thảo mãn
* Trường hợp 1: Có 2 học sinh khá:
- Có 3 cách chọn 1 học sinh giỏi.
- Có C\(\frac{2}{5}\) = 10 cách chọn 2 học sinh khá.
- Có C\(\frac{5}{8}\) = 56 cách chọn 5 học sinh trung bình.
=> Có: 3.10.56 = 16803.10.56 = 1680 cách.
* Trường hợp 2: Có 3 học sinh khá:
- Có 3 cách chọn 1 học sinh giỏi.
- Có C\(\frac{3}{5}\) = 10 cách chọn 3 học sinh khá.
- Có C\(\frac{4}{8}\) = 70 cách chọn 4 học sinh trung bình.
=> Có: 3.10.70 = 21003.10.70 = 2100 cách.
Vậy có tất cả: 1680+2100 = 37801680+2100 = 3780 cách