
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TV
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
0

L
1

5 tháng 10 2015
1
1+2+3+4+...+n thì cũng là 1+2+3+4+..+(n-2)+(n-1)+n.
giờ ta nhóm số đầu với số cuối, số thứ 2 với số gần cuối.
cụ thể là (1+n)+(2+n-1)+(3+n-2)+... có n/2 số tổng như thế.
suy ra kết quả là (n+1)n/2 nha bạn.
2.
tương tự như bài 1,m chỉ việc nhóm 2 ra đầu là thành bài 1
kết quả sẽ là n(n+1).
3.
bài 3 tương tự như bài 1 thôi.
nhóm (1 và 2n+1) thành 1 nhóm, (3 và 2n-1) thành 1 nhóm... câu 3 trở thành 2(n+1)+n(n+1)...có n/2 số như thế.
kết quả sẽ là n(n+1).
A.Lý thuyết về dấu tam thức bậc hai
1. Tam thức bậc hai (một ẩn) là đa thức có dạng f(x) = ax2 + bx + c trong đó x là biến a, b, c là các số đã cho, với a ≠ 0.
Định lí. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0)
có biệt thức ∆ = b2 – 4ac.
- Nếu ∆ < 0 thì với mọi x, f(x) có cùng dấu với hệ số a.
- Nếu ∆ = 0 thì f(x) có nghiệm kép x =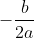 , với mọi x ≠
, với mọi x ≠ 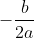 , f(x) có cùng dấu với hệ số a.
, f(x) có cùng dấu với hệ số a.
- Nếu ∆ > 0, f(x) có 2 nghiệm x1, x2 (x1 < x2) và luôn cùng dấu với hệ số a với mọi x ngoài đoạn [x1; x2] và luôn trái dấu với hệ số a với mọi x trong đoạn (x1; x2).
2. Bất phương trình bậc hai một ẩn.
Là mệnh đề chứa một biến có một trong các dạng:
ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx + c ≥ 0, ax2 + bx + c ≤ 0 trong đó vế trái là một tam thức bậc hai.
Để giải bất phương trình bậc hai một ẩn ta dùng định lí về dấu của tam thức bậc hai.