Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
8:
\(=\dfrac{cos10-\sqrt{3}\cdot sin10}{sin10\cdot cos10}=\dfrac{2\left(\dfrac{1}{2}\cdot cos10-\dfrac{\sqrt{3}}{2}\cdot sin10\right)}{sin20}=\dfrac{sin\left(30-10\right)}{sin20}=1\)
10:
\(=\left(2-\sqrt{3}\right)^2+\left(2+\sqrt{3}\right)^2\)
=7-4căn 3+7+4căn 3=14
12:
\(=cos^270^0+\dfrac{1}{2}\left[cos60-cos140\right]\)
\(=cos^270^0+\dfrac{1}{2}\cdot\dfrac{1}{2}-\dfrac{1}{2}\cdot2cos^270^0+\dfrac{1}{.2}\)
=1/4+1/2=3/4
\(\dfrac{2sin8a-sin16a}{2sin8a+sin16a}=\dfrac{2sin8a-2sin8a.cos8a}{2sin8a+2sin8a.cos8a}=\dfrac{2sin8a\left(1-cos8a\right)}{2sin8a\left(1+cos8a\right)}=\dfrac{1-cos8a}{1+cos8a}=\dfrac{1-\left(1-2sin^24a\right)}{1+\left(1-2sin^24a\right)}=\dfrac{2sin^24a}{2-2sin^24a}=\dfrac{sin^24a}{1-sin^24a}=\dfrac{sin^24a}{cot^24a}=tan^24a\)
\(=\dfrac{2sin8a-2sin8a.cos8a}{2sin8a+2sin8a.cos8a}=\dfrac{2sin8a\left(1-cos8a\right)}{2sin8a\left(1+cos8a\right)}=\dfrac{1-cos8a}{1+cos8a}\)
\(=\dfrac{1-\left(1-2sin^24a\right)}{1+\left(2cos^24a-1\right)}=\dfrac{2sin^24a}{2cos^24a}=tan^24a\)
3:
\(=\dfrac{2}{1+cotx-tanx-1}=\dfrac{2}{cotx-tanx}\)
\(=2:\left(\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}\right)=2:\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}\)
\(=\dfrac{sin2x}{cos2x}\)
=tan2x
4:
\(=\left(1-\dfrac{1}{cot^2x}\right)\cdot cotx=cotx-\dfrac{1}{cotx}=\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}\)
\(=\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}=\dfrac{cos2x}{\dfrac{1}{2}\cdot2\cdot sinx\cdot cosx}=\dfrac{cos2x}{sin2x}\cdot2\)
6:
\(=\dfrac{\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}}{cos2x}=\dfrac{cos^2x-sin^2x}{sinx\cdot cosx}:cos2x=\dfrac{1}{sinx\cdot cosx}\)
10.
\(\dfrac{sin3x-cos3x}{sinx+cosx}=\dfrac{3sinx-4sin^3x-\left(4cos^3x-3cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sin^3x+cos^3x\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(1-sinx.cosx\right)}{sinx+cosx}\)
\(=\dfrac{\left(sinx+cosx\right)\left(3-4+4sinx.cosx\right)}{sinx+cosx}\)
\(=-1+4sinx.cosx\)
\(=2sin2x-1\)
11.
\(tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\dfrac{1+cos\left(\dfrac{\pi}{2}+x\right)}{sin\left(\dfrac{\pi}{2}+x\right)}=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{1+sin\left(-x\right)}{cos\left(-x\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{1-sinx}{cosx}=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\dfrac{sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}-2sin\dfrac{x}{2}cos\dfrac{x}{2}}{cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{\left(cos\dfrac{x}{2}-sin\dfrac{x}{2}\right)^2}{\left(cos\dfrac{x}{2}-sin\dfrac{x}{2}\right)\left(cos\dfrac{x}{2}+sin\dfrac{x}{2}\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{cos\dfrac{x}{2}-sin\dfrac{x}{2}}{cos\dfrac{x}{2}+sin\dfrac{x}{2}}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{cos\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}{sin\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).cot\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\)
\(=1\)
5:
a: sin x=2*cosx
\(A=\dfrac{6cosx+2cosx-4\cdot8\cdot cos^3x}{cos^3x-2cosx}\)
\(=\dfrac{8-32cos^2x}{cos^2x-2}\)
b: VT=sin^4(pi/2-x)+cos^4(x+pi/2)+6*1/2*sin^22x+1/2*cos4x
=cos^4x+sin^4x+3*sin^2(2x)+1/2*(1-2*sin^2(2x))
=1-2*sin^2x*cos^2x+3*sin^2(2x)+1/2-sin^2(2x)
==3/2=VP
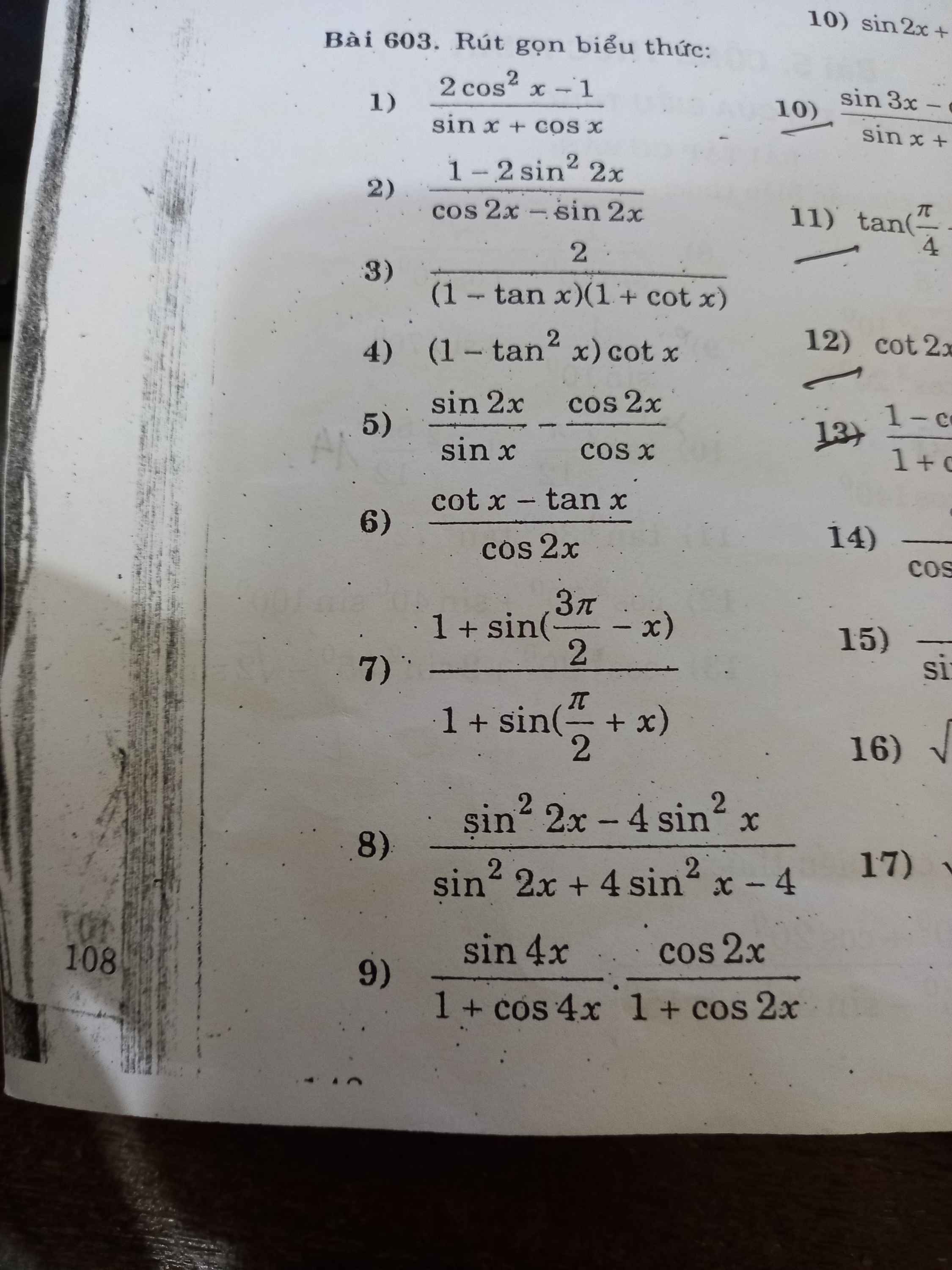
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
Đề bài yêu cầu điều gì em nhỉ?
dạ là rút gọn biểu thức ạ