
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
=10-7=3
Bài 3:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{7}=\dfrac{y}{3}=\dfrac{x-y}{7-3}=\dfrac{-16}{4}=-4\)
Do đó: x=-28; y=-12
Ax // BC // Dy. A= 55°
a) Tính B = ?
b) Tìm số đo của C để AB//CD. Khi đó tính D =?
Giúp tớ với huhu :(


Cho a/b = c/d > Chứng minh
a)\(\frac{a^2-b^2}{c^2-d^2}=\frac{ab}{cd}\)
b)\(\frac{\left(a-b\right)^2}{\left(c-d\right)^2}=\frac{ab}{cd}\)\
GIẢI :
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{ab}{cd}=\frac{a}{c}.\frac{a}{c}=\frac{b}{d}.\frac{b}{d}=\frac{a^2-b^2}{c^2-d^2}\)
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\Rightarrow\frac{ab}{cd}=\frac{a}{c}.\frac{b}{d}=\frac{a-b}{c-d}.\frac{a-b}{c-d}=\frac{\left(a-b\right)^2}{\left(c-d\right)^2}\)


b,\(\left|x\right|=\dfrac{1}{3}\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Thay \(x=\dfrac{1}{3},y=-3\) vào B ta có:
\(B=2x^2-3xy+4y^2=2.\left(\dfrac{1}{3}\right)^2-3.\dfrac{1}{3}.\left(-3\right)+4.\left(-3\right)^2=2.\dfrac{1}{9}+3+4.9=\dfrac{2}{9}+3+36=\dfrac{353}{9}\)
Thay \(x=\dfrac{-1}{3},y=-3\) vào B ta có:
\(B=2x^2-3xy+4y^2=2.\left(\dfrac{-1}{3}\right)^2-3.\dfrac{-1}{3}.\left(-3\right)+4.\left(-3\right)^2=2.\dfrac{1}{9}-3+4.9=\dfrac{2}{9}-3+36=\dfrac{299}{9}\)
d,\(D=5\left(x-3\right)+4\left(2-x\right)=5x-15+8-4x=x-7\)
\(x^2=4\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
Thay x=-2 vào D ta có:
\(D=x-7=-2-7=-9\)
Thay x=2 vào D ta có:
\(D=x-7=2-7=-5\)
e,Thay x=2 vào E ta có:
\(\dfrac{2x^2-5x+6}{x-3}=\dfrac{2.2^2-5.2+6}{2-3}=\dfrac{8-10+6}{-1}=-4\)
f, Đặt \(\dfrac{x}{3}=\dfrac{y}{5}=k\Rightarrow x=3k,y=5k\)
\(F=\dfrac{5x^2+3y^2}{10x^2-3y^2}=\dfrac{5.\left(3k\right)^2+3.\left(5k\right)^2}{10.\left(3k\right)^2-3.\left(5k\right)^2}=\dfrac{5.9k^2+3.25k^2}{10.9k^2-3.25k^2}=\dfrac{45k^2+75k^2}{90k^2-75k^2}=\dfrac{120}{15}=8\)

Bài 5:
a: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)
MC=MB
Do đó: ΔMAC=ΔMDB
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AC//BD


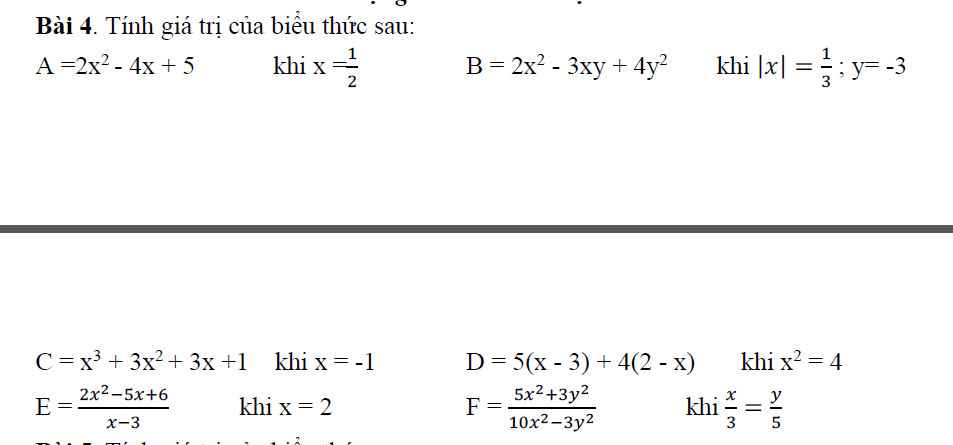 giúp tớ câu B, D, E, F với huhu
giúp tớ câu B, D, E, F với huhu
 :
:
\(4x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{4}\)
Mà \(\dfrac{x}{3}=\dfrac{z}{5}\Rightarrow\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
\(\Rightarrow\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{z^2}{25}\Rightarrow\dfrac{2x^2}{18}=\dfrac{2y^2}{32}=\dfrac{3z^2}{75}=\dfrac{2x^2+2y^2-3z^2}{18+32-75}=\dfrac{-100}{-25}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=36\\y^2=64\\z^2=100\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left(x;y;z\right)=\left(6;8;10\right)\\\left(x;y;z\right)=\left(-6;-8;-10\right)\end{matrix}\right.\)