Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





B3
1) \(\sqrt{ }\)(2x-1)2 =5
\(\Leftrightarrow\) |2x-1| =5
\(\Leftrightarrow\) 2x-1 =5 hoặc 2x -1 = -5
\(\Leftrightarrow\) 2x=6 hoặc 2x= -4
\(\Leftrightarrow\) x=3 hoặc x= -2
2) 4-5x = 144
\(\Leftrightarrow\) -5x =140
\(\Leftrightarrow\) x= -60
3) \(\sqrt{ }\)(2x-2)2=2x-2
\(\Leftrightarrow\) | 2x -2 | =2x-2
\(\Leftrightarrow\) 2x-2 =2x-2 hoặc 2x-2 =-2x +2
\(\Leftrightarrow\) 0x=0 (loại ) hoặc x=2 ( nhận )

Bạn nên tách lẻ các bài ra post riêng. Đăng thế này chiếm diện tích, khó quan sát => mọi người dễ bỏ qua bài của bạn.

có
<=>352=2\(\pi\).7.h<=>352=14\(\pi\).h<=>h=352/(14.\(\pi\))
<=>h\(\approx\)8cm( nếu lấy\(\pi\) \(\approx\)3,14)

Lời giải:
Cộng 3 PT lại ta có:
$x(a+b+c)+y(a+b+c)=a+b+c$
$\Leftrightarrow (a+b+c)(x+y-1)=0$
$\Rightarrow a+b+c=0$ hoặc $x+y-1=0$
TH1: $a+b+c=0\Leftrightarrow a+b=-c$
Khi đó: $a^3+b^3+c^3=(a+b)^3-3ab(a+b)+c^3$
$=(-c)^3-3ab(-c)+c^3=3abc$
$\Rightarrow \frac{a^2}{bc}+\frac{b^2}{ac}+\frac{c^2}{ab}=3$ (đpcm)
TH2: $x+y-1=0\Leftrightarrow y=1-x$
Thay vô hpt \(\left\{\begin{matrix} ax+b(1-x)=c\\ bx+c(1-x)=a\\ cx+a(1-x)=b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x(a-b)=c-b\\ x(b-c)=a-c\\ x(c-a)=b-a\end{matrix}\right.\)
\(\Rightarrow x^3(a-b)(b-c)(c-a)=(c-b)(a-c)(b-a)=-(a-b)(b-c)(c-a)\)
\(\Leftrightarrow (a-b)(b-c)(c-a)(x^3+1)=0\)
Nếu $a-b=0$ thì kéo theo $b-c=c-a=0$
$\Rightarrow a=b=c$
Nếu $b-c=0; c-a=0$ thì tương tự
Nếu $x^3+1=0\Leftrightarrow x=-1$
$\Rightarrow b-a=c-b=a-c\Rightarrow a=b=c$
Tóm lại $a=b=c$
Do đó: $\frac{a^2}{bc}+\frac{b^2}{ac}+\frac{c^2}{ab}=1+1+1=3$ (đpcm)


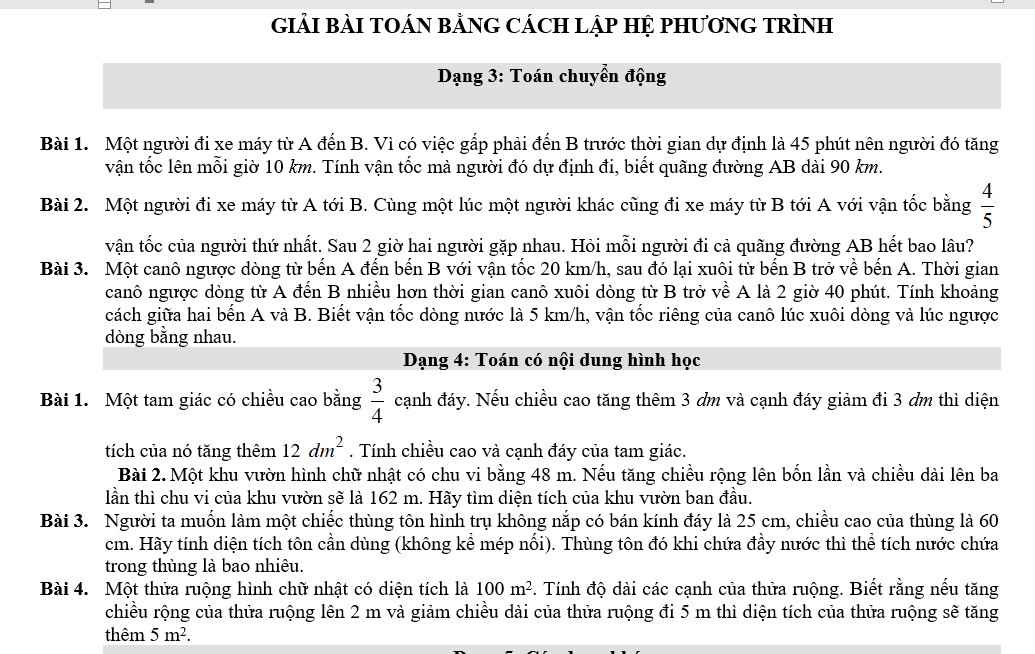 các bạn giúp mình với mình đang cần gấp
các bạn giúp mình với mình đang cần gấp