Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Cách giải:
![]()
![]()
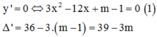
+ ![]() => Hàm số đồng biến trên
=> Hàm số đồng biến trên ![]()
+ ![]() Phương trình (1) có 2 nghiệm phân biệt
Phương trình (1) có 2 nghiệm phân biệt ![]()
Theo đinh lí Viet ta có 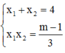
Khi đó, để hàm số đồng biến trên khoảng (1;+∞) thì
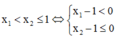
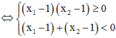
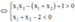
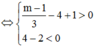 ( vô lí )
( vô lí )
Vậy m ≥ 13
Mà ![]()
![]()
Số giá trị của m thỏa mãn là: 2018 - 13 + 1 = 2006

Đáp án B
Ta có y ' = 4 sin 2 x cos x sin x - ( 2 m 2 - 5 m + 2 ) cos x = cos x [ ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ]
Xét trên ( 0 ; π 2 ) ta thấy cos x > 0 , để hàm số đồng biến trên khoảng này thì ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ≥ 0 với ∀ x ∈ ( 0 ; π 2 ) hay ( 2 m 2 - 5 m + 3 ) ≤ 0 ⇒ 1 ≤ m ≤ 3 2 do m nguyên nên tồn tại duy nhất m=1

Đáp án C
Ta có y ' = − m 2 + 2016 m + 2017 x + m 2 , y ' = 0 đồng biến trên từng khoảng xác định nếu
y ' > 0 ∀ x ∈ D ⇔ − m 2 + 2016 m + 2017 > 0 ⇔ m ∈ − 1 ; 2017
Ta đếm số nguyên trong
− 1 ; 2017 thì có 2016 số nguyên trong đó.


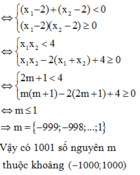
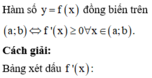

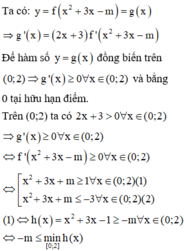
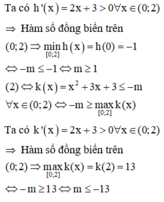



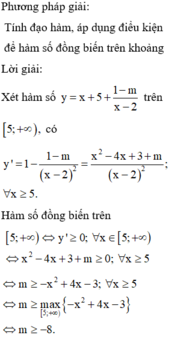
Đáp án A
Để hàm số đồng biến trên khoảng 2 ; + ∞ thì
Xét f x = 3 x 2 − 6 x + 5 12 x − 1 có đạo hàm f ' x = 3 x 2 − 6 x + 1 12 x − 1 2 > 0 x > 2
Do đó f(x) đồng biến trên khoảng 2 ; + ∞ hay M i n f x = f 2 = 5 12 ⇒ m < 5 12
Lại có m ∈ − 2017 ; 2017 m ∈ ℤ .
Suy ra có 2018 giá trị của m thỏa mãn