DK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DK
1
LK
11 tháng 9 2016
Vì hình thang ABCD cân => AB // CD => góc DAC= góc BAC
Xét tam giác ADC và tam giác CAB
Ta có: AB=AD (gt), góc DAC=BAC(cmt), AD=BC(hình thang ABC cân)
=> tam giác ADC=tam giác CAB(c-g-c)
=> góc BCA= góc DCA ( 2 góc t.ứng)
=> AC là tia p/g của góc C
PT
1
CM
12 tháng 11 2019
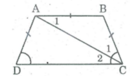
Ta có:
AB = AD (gt)
AD = BC (tính chất hình thang cân)
⇒ AB = BC do đó ΔABC cân tại B
⇒ ∠ BAC = ∠ BCA (tính chất tam giác cân) (*)
ABCD là hình thang có đáy là AB nên AB // CD
∠ BAC = ∠ DCA (hai góc so le trong) (**)
Từ (*) và (**) suy ra: ∠ BCA = ∠ DCA (cùng bằng ∠ BAC)
Vậy CA là tia phân giác của ∠ BCD.
NT
0
SG
1
27 tháng 7 2017
Ta có: \(AB = AD\)
Mà \(AD = BC\) (ABCD là hình thang cân)
\(\Rightarrow AB=BC\)
Nối A và C
Ta có: \(AB=BC\Rightarrow\Delta ABC\) là \(\Delta\) cân \(\Rightarrow\widehat{BAC}=\widehat{BCA}\) (1)
Ta lại có: AB // CD (ABCD là hình tang cân)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\) ( cặp góc so le trong) (2)
Từ (1) và (2) \(\Rightarrow\widehat{BCA}=\widehat{ACD}\Rightarrow CA\) là phân giác của \(\widehat{C}\) (ĐPCM)
26 tháng 9 2021
Ta có: AB=AD
mà AD=BC
nên BA=BC
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{BCA}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
CM
2
27 tháng 6 2016
vì ABCD là hình thang cân nên ta có AD=BC(hai cạnh bên)
mà theo bài ra AB=AD => AB=AD=BC
=> tam giác ABC cân tại B => góc BAC= góc BCA(hai góc đáy)
mặt khác ta có góc BAC = góc ACD ( so le trong)
=> góc BCA = góc ADC => CA là tia phân giác góc C
GH
22 tháng 6 2023
2)
Có: \(\left\{{}\begin{matrix}AB=AD\left(gt\right)\\AD=BC\left(2.cạnh.bên.hình.thang.cân\right)\end{matrix}\right.\)
\(\Rightarrow AB=BC\Rightarrow\Delta ABC.cân.tại.B\)
Mà AB // ED (gt)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\left(so.le.trong\right)\)
\(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
=> CA là tia phân giác của góc C.
15 tháng 9 2016
hình hơi xấu với lại chưa cân bạn thông cảm nha
do AB =AD mà BC = AD nên BC = AB => tam giác ABC cân tại B => góc BAC = góc BCA (1)
do ABCD là hình thang nên góc BAC =góc ACD (2)
Từ (1) và (2) => góc BCA =góc ACD => CA là tia phân giác của góc BCD => đpcm
Dễ mà
Ta có: AB = AD
Mà AD = BC ( vì ABCD là hình thang cân)
=> AB = BC
Nối A và C lại vs nhau
Ta có: AB = BC => tamm giác ABC là tam giác cân => góc BAC = góc BCA (1)
Ta lại có: AB // CD ( ABCD là hình tang cân)
=> Góc BAC = góc ACD ( cặp góc so le trong) (2)
Từ (1) và (2)
=> Góc BCA = góc ACD => CA là phân giác của góc C