Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính
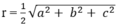
Do đó diện tích mặt cầu (S) là: S = 4 πr 2 = π( a 2 + b 2 + c 2 )

Chọn B.
Giả sử khối hộp chữ nhật có ba kích thước là a, b, c.
Khi đó thể tích khối hộp chữ nhật là: V = abc.
Từ giả thiết ta có
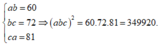
![]()
Vậy thể tích V của khối hình hộp chữ nhật gần nhất với giá trị 592.

Chọn A.
Tâm của mặt cầu chính là tâm của của hình hộp chữ nhật.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật.
Mà độ dài đường chéo của hình chữ nhật là ![]() nên mặt cầu (S) có bán kính
nên mặt cầu (S) có bán kính
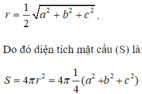
![]()

Gọi H là hình chiếu vuông góc của A' trên mặt phẳng (ABCD)
Kẻ HN vuông góc với AB tại N, HM vuông góc với AD tại M
Ta cần tìm chiều cao h=A'H của hình hộp
Dễ dàng chứng minh \(\widehat{A'NH}=60^0\) và \(\widehat{A'MH}=45^0\)
Xét tam giác vuông NHA' và MHB' có
\(NH=\frac{HA'}{tan\widehat{HNA'}}=\frac{h}{\sqrt{3}}\) và \(MH=\frac{HA'}{tan\widehat{HMA'}}=h\)
Xét hình vuông AMHN có \(AH=\sqrt{HN^2+HM^2}=\frac{2h}{\sqrt{3}}\)
Xét tam giác vuông AHA' có \(AH^2+A'H^2=A'A^2\Leftrightarrow h^2+\frac{4}{3}h^2=1\Leftrightarrow h=\sqrt{\frac{3}{7}}\)
Vậy thể tích hình hộp là: \(V=h.\sqrt{3}.\sqrt{7}=\sqrt{\frac{3}{7}}.\sqrt{3}\sqrt{7}=3\)

Chọn A.
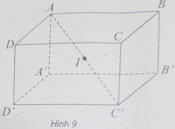
(h.9) Tâm của hình hộp chữ nhật cách đều 8 đỉnh của hình hộp nên tâm của mặt cầu (S) chính là tâm của hình hộp chữ nhật.

Chọn D.
Tâm của hình hộp chữ nhật cách đều 8 đỉnh của hình hộp nên tâm của mặt cầu (S) chính là tâm của hình hộp chữ nhật.
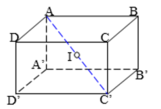

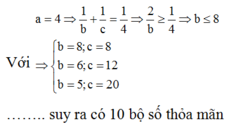

Chọn C
Thể tích hình hộp đó là V = 3.4.5 = 60