Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
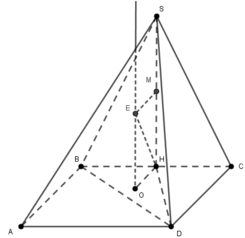
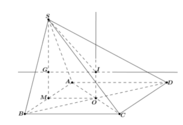
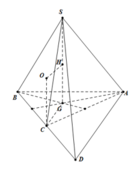
Gọi R và r lần lượt là bán kính mặt cầu ngoại tiếp hình chóp S. BHD và tam giác BHD.
Ta có HB= a 2 2 , H D = H C 2 + D C 2 = a 2 2 2 + a 2 = a 6 2 , B D = a 2 + 2 a 2 = a 3
Áp dụng định lí Cô sin, ta có
cos B H D ^ = a 2 2 + 3 a 2 2 - 3 a 2 2 . a 2 2 a 6 2 = - 1 3 ⇒ sin B H D ^ = 2 3
Diện tích tam giác BHD là
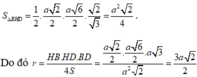
Gọi O là tâm đường tròn ngoại tiếp tam giác BHD và M là trung điểm SH. Mặt phẳng trung trực của SH cắt trục đường tròn ngoại tiếp tam giác BHD tại E. Khi đó E là tâm mặt cầu cần tìm.
Ta có
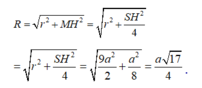

Gọi \(I\) là tâm của đáy \(ABCD\) (giao điểm của \(AC\) và \(BD\))
a) Vì đây là hính chóp đều nên có ngay \(SI\) là đường cao kẻ từ S
\(SI=\sqrt{SA^2-AI^2}=\sqrt{SA^2-\frac{AB^2}{2}}=a\sqrt{2}\)
\(V_{S.ABCD}=\frac{1}{3}.SI.S_{ABCD}=\frac{4a^3\sqrt{2}}{3}\)
b) Thấy ngay \(IA=IB=IC=ID=IS=a\sqrt{2}\)
suy ra tâm mc ngoại tiếp là \(I\) và \(R=a\sqrt{2}\)
c) bạn dùng công thức sau để tính bán kính mặt cầu nội tiếp
\(r=\frac{3V_{S.ABCD}}{S_{ABCD}+4S_{SAB}}=\frac{\frac{4a^3\sqrt{2}}{3}}{4a^2+4.\frac{a^2\sqrt{3}}{2}}=\frac{4\sqrt{2}-2\sqrt{6}}{3}.a\)
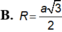
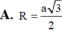
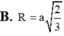
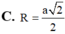


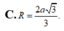
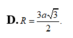


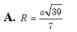
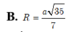
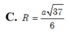
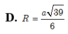


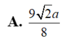
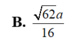
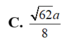
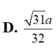
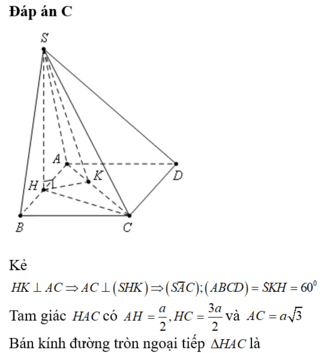

Chọn C