Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
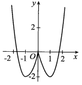
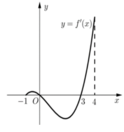
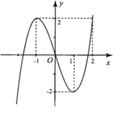
Từ đồ thị hàm số đã cho (như hình vẽ) ta suy ra đồ thị của hàm số
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán
: 
+ Trước tiên từ đồ thị hàm số y= f( x) , ta suy ra đồ thị hàm số y = |f(x)| như hình dưới đây:
Phương trình 2|f(x)| - m = 0 hay |f(x)| = m/2 là phương trình hoành độ giao điểm của đồ thị hàm số y = |f(x) và đường thẳng y= m/2.
Dựa vào đồ thị hàm số y = |f(x)|, ta có ycbt trở thành:
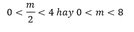
Chọn A.
Đáp án A
(*)
Đặt 
Yêu cầu bài toán trở thành: Tìm m để phương trình 
có nghiệm 
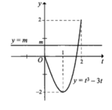
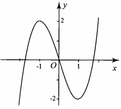
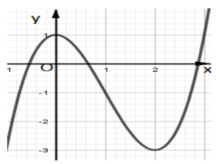
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số 
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán 
Chọn đáp án D.
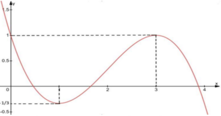
Do đó để phương trình f sin x = m có nghiệm trong khoảng (0;p)
thì phương trình f t = m có nghiệm t ∈ ( 0 ; 1 ]
Đáp án D
Phương pháp:
Số nghiệm của phương trình |f(x)| = m bằng số giao điểm của đồ thị hàm số y = |f(x)| và đường thẳng y = m
Cách giải:
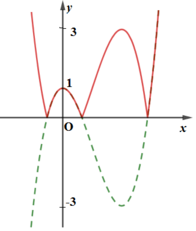
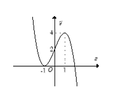
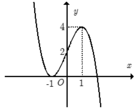
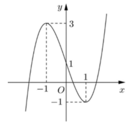
Từ đồ thị hàm số y = f(x) ta có đồ thị hàm số y = |f(x)| như hình bên:
Số nghiệm của phương trình |f(x)| = m bằng số giao điểm của đồ thị hàm số y = |f(x)| và đường thẳng y = m
⇒ Để phương trình |f(x)| = m có 4 nghiệm phân biệt thì 1 < m < 3
Đáp án A
Đặt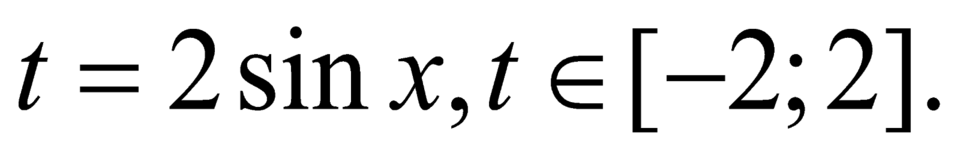
Yều cẩu bào toán trở thành: Tìm m để bất phương trình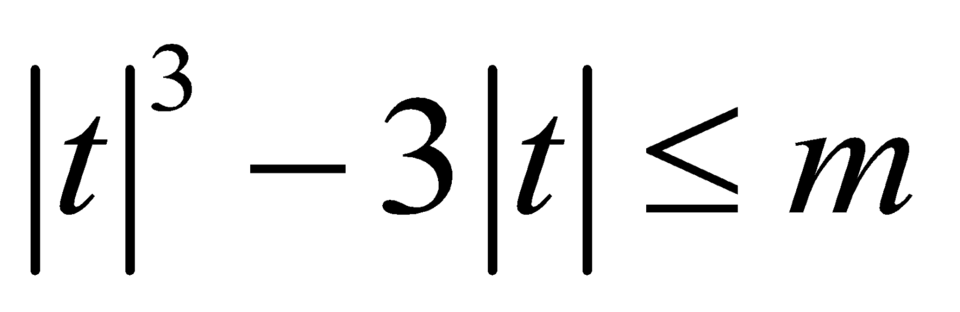
nghiệm đúng với mọi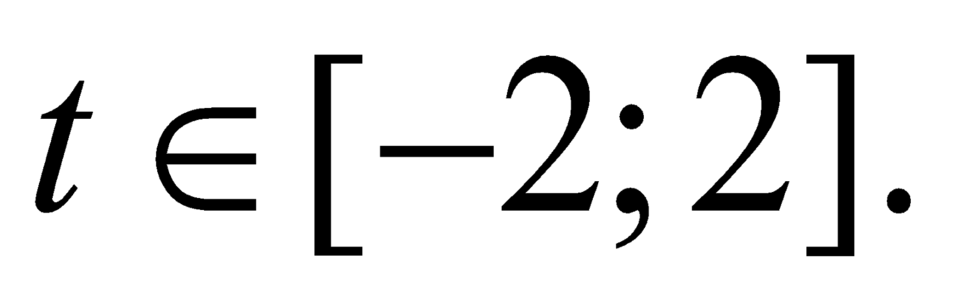 
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số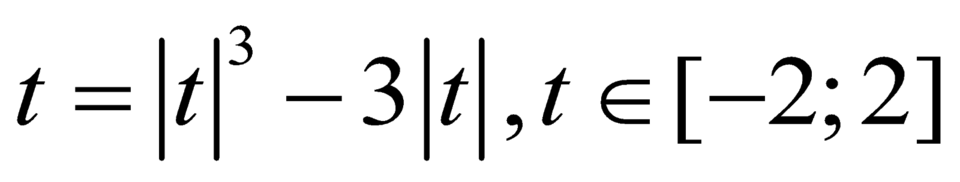
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán là