Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(\left\{{}\begin{matrix}a=\sqrt{x-3}\\b=\sqrt{9-2x}\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow ab=\sqrt{-2x^2+15x-27};a^2+b^2=-x+6\)
\(PT\Leftrightarrow a+b=2ab+a^2+b^2+2\\ \Leftrightarrow\left(a+b\right)^2-\left(a+b\right)-2=0\\ \Leftrightarrow\left(a+b\right)^2+\left(a+b\right)-2\left(a+b\right)-2=0\\ \Leftrightarrow\left(a+b\right)\left(a+b+1\right)-2\left(a+b+1\right)=0\\ \Leftrightarrow\left(a+b-2\right)\left(a+b+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a+b=2\left(n\right)\\a+b=-1\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow a+b=2\\ \Leftrightarrow\sqrt{x-3}=2-\sqrt{9-2x}\left(3\le x\le\dfrac{9}{2}\right)\\ \Leftrightarrow x-3=11-2x-4\sqrt{9-2x}\\ \Leftrightarrow x+14=4\sqrt{9-2x}\\ \Leftrightarrow x^2+28x+196=144-32x\\ \Leftrightarrow x^2+60x+52=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-30+4\sqrt{53}\left(l\right)\\x=-30-4\sqrt{53}\left(l\right)\end{matrix}\right.\)
Vậy PT vô nghiệm





Câu 5:
Áp dụng định lí cos: \(bc\cdot\cos A=bc\cdot\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{b^2+c^2-a^2}{2}\)
Tương tự \(\Leftrightarrow ac\cdot\cos B=\dfrac{c^2+a^2-b^2}{2};ab\cdot\cos C=\dfrac{a^2+b^2-c^2}{2}\)
\(\Leftrightarrow P=\dfrac{a^2+b^2-c^2+b^2+c^2-a^2+c^2+a^2-b^2}{2}=\dfrac{a^2+b^2+c^2}{2}=\dfrac{4032}{2}=2016\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-2y+z=2\\4y-4z=-6\\-y+z=-13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y+z=2\\y-z=-\dfrac{3}{2}\\-y+z=-13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y+z=2\\y-z=-\dfrac{3}{2}\\0=-\dfrac{29}{2}\end{matrix}\right.\)
Hệ đã cho vô nghiệm



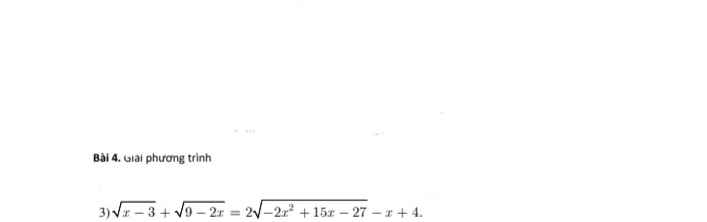
 Help me. Cần gấp😔😞😞😞
Help me. Cần gấp😔😞😞😞