K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 8 2021
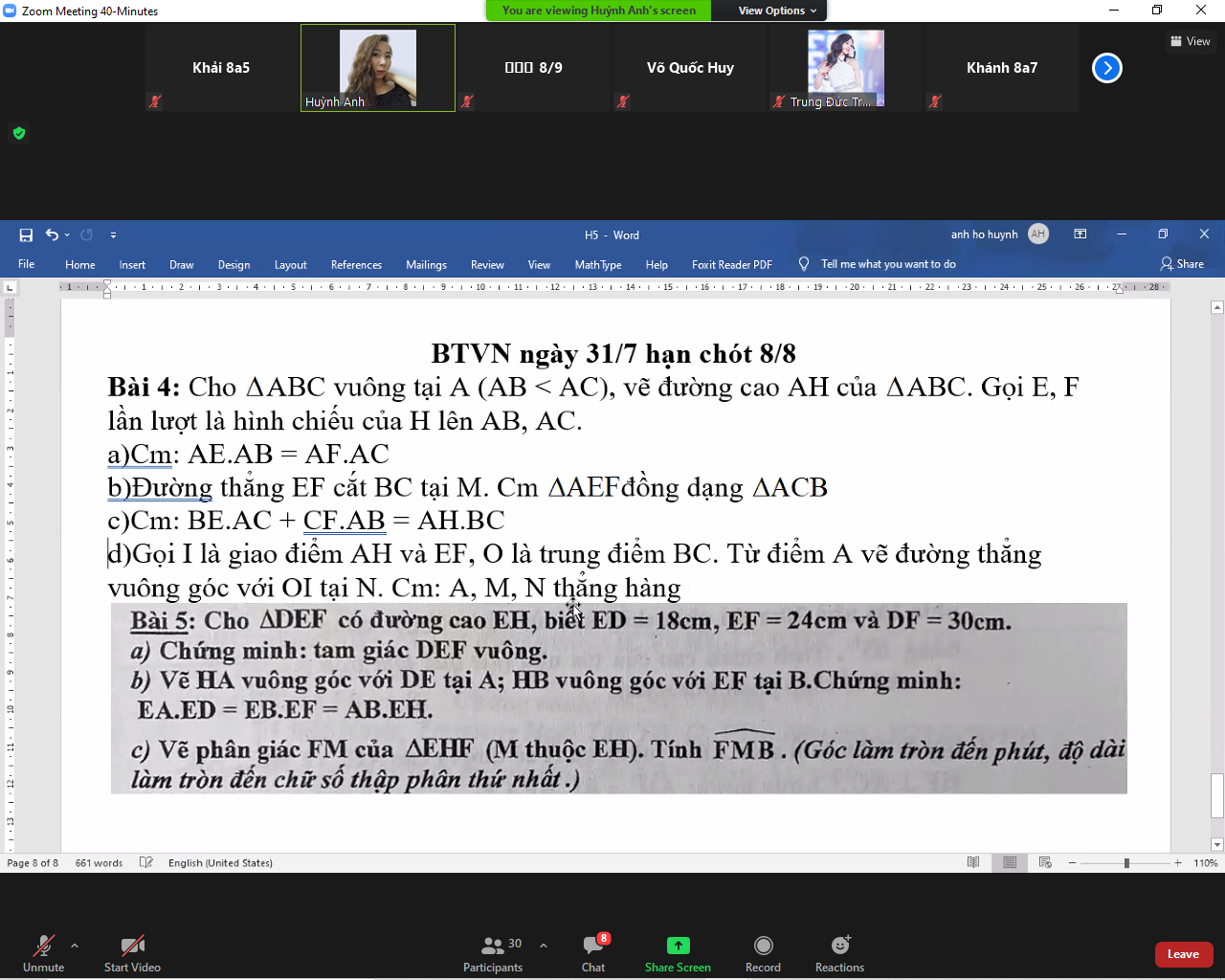
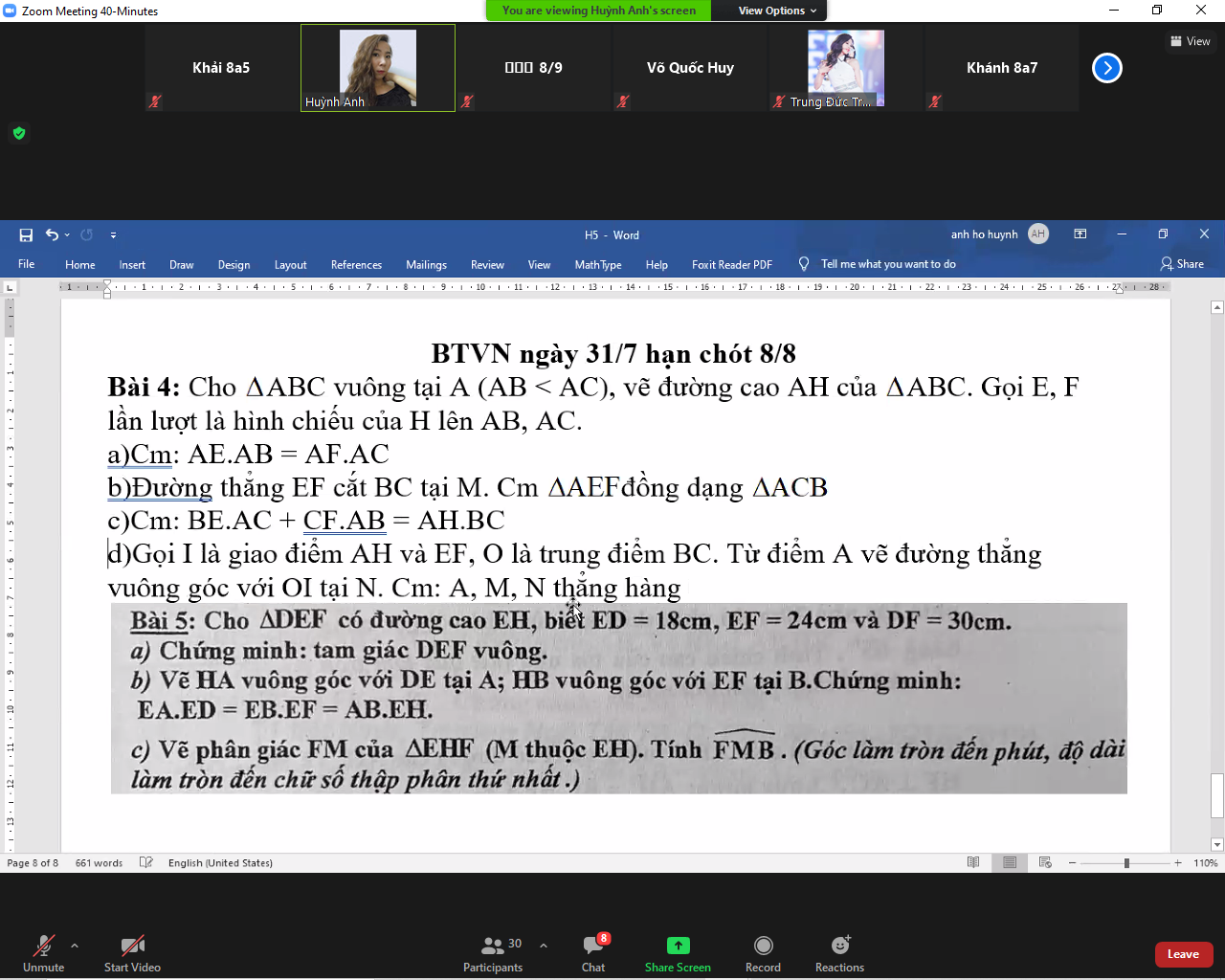
Bài 4:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
19 tháng 8 2021
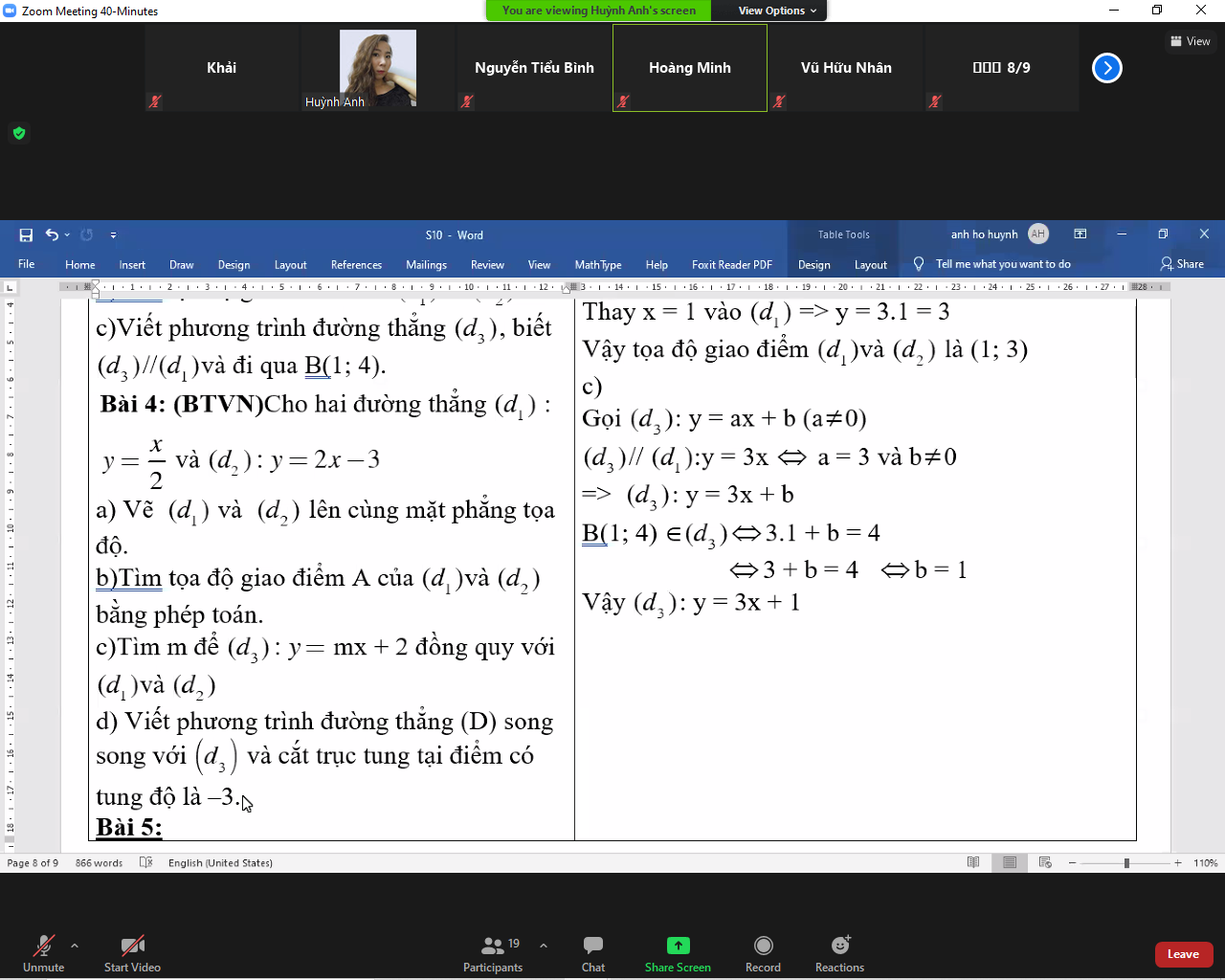
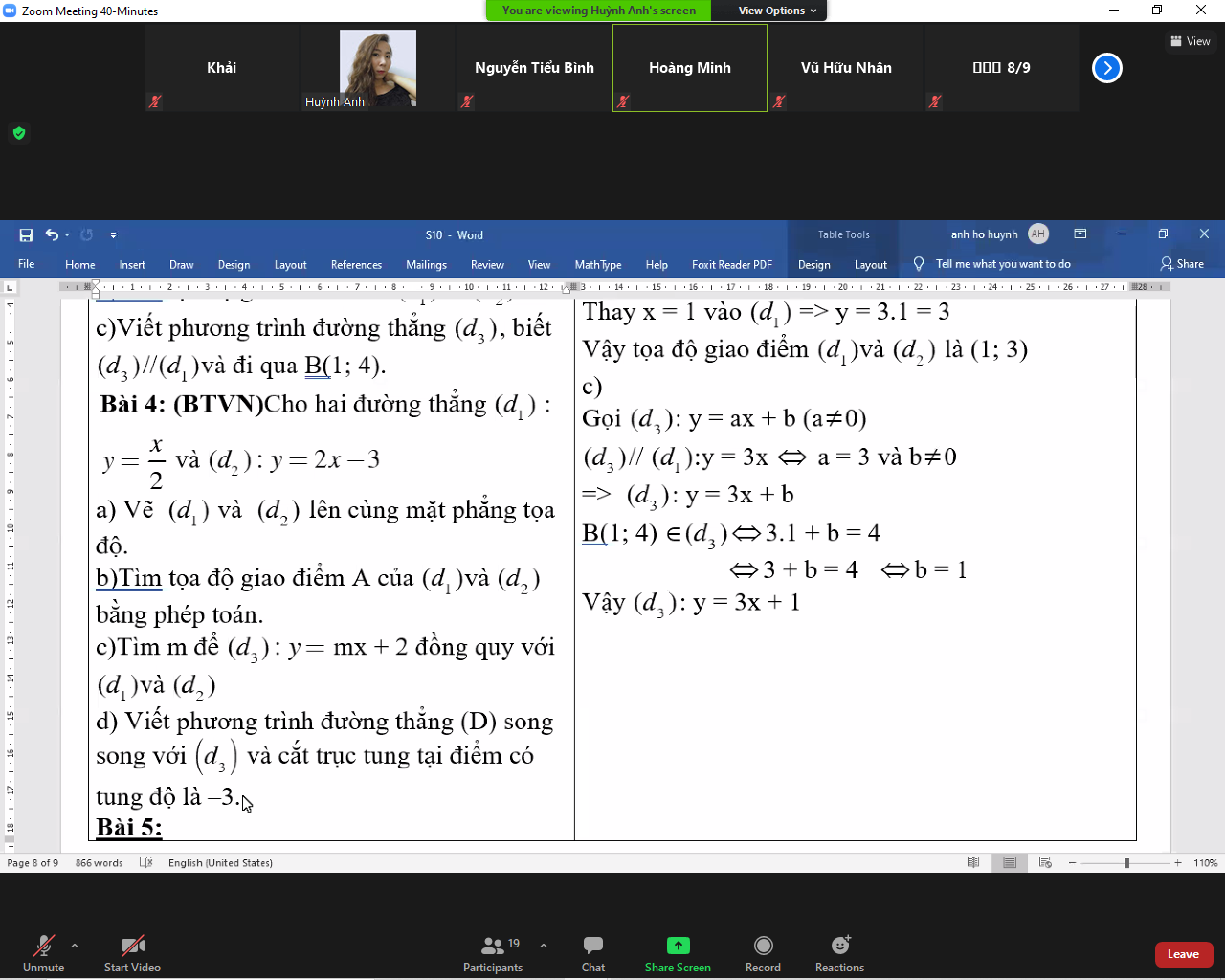
Bài 4:
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x=2x-3\)
\(\Leftrightarrow x\cdot\dfrac{-3}{2}=-3\)
hay x=2
Thay x=2 vào hàm số y=2x-3, ta được:
\(y=2\cdot2-3=1\)
c: Thay x=2 và y=1 vào y=mx+2, ta được:
\(2m+2=1\)
\(\Leftrightarrow2m=-1\)
hay \(m=-\dfrac{1}{2}\)
AH
Akai Haruma
Giáo viên
29 tháng 5 2023
Lời giải:
Đổi 30 phút = 0,5 giờ và 4 giờ 6 phút =4,1 giờ
Gọi vận tốc riêng của cano là $x$ km/h ($x>3$) thì:
Vận tốc xuôi dòng: $x+3$ (km/h)
Vận tốc ngược dòng: $x-3$ (km/h)
Tổng thời gian đi và về:
$\frac{48}{x+3}+\frac{48}{x-3}=4,1-0,5=3,6$
$\Leftrightarrow \frac{1}{x+3}+\frac{1}{x-3}=\frac{3}{40}$
$\Leftrightarrow \frac{2x}{x^2-9}=\frac{3}{40}$
$\Leftrightarrow 3x^2-27-80x=0$
$\Leftrightarrow (x-27)(3x+1)=0$
$\Rightarrow x=27$ (do $x>3$)
Vậy.......
help em cau 3 vs
31 tháng 7 2021
Câu 2:
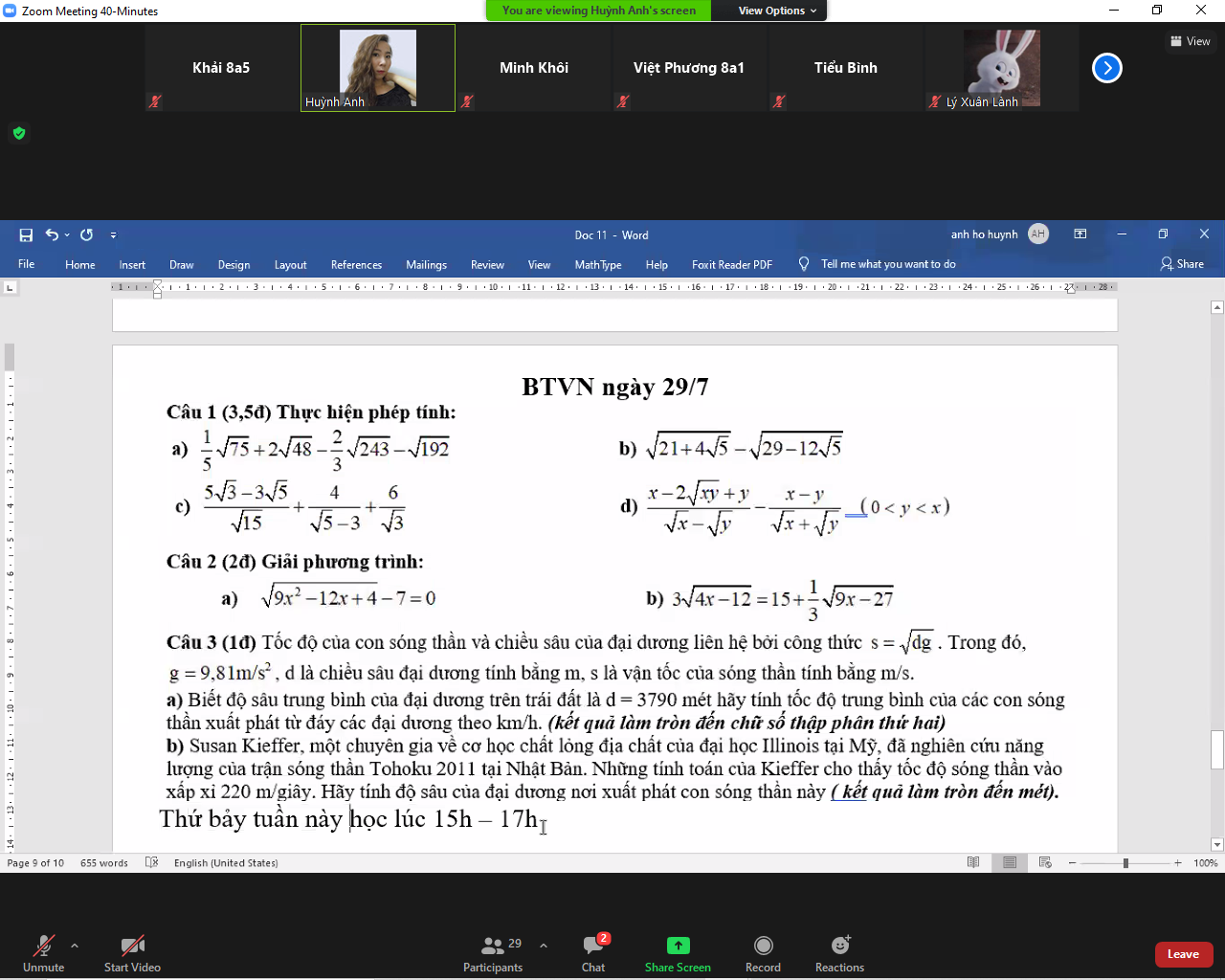
a) Ta có: \(\sqrt{9x^2-12x+4}-7=0\)
\(\Leftrightarrow\left|3x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-2=7\\3x-2=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=9\\3x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{3}\end{matrix}\right.\)
b) Ta có: \(3\sqrt{4x-12}=15+\dfrac{1}{3}\sqrt{9x-27}\)
\(\Leftrightarrow6\sqrt{x-3}-\sqrt{x-3}=15\)
\(\Leftrightarrow5\sqrt{x-3}=15\)
\(\Leftrightarrow\sqrt{x-3}=3\)
\(\Leftrightarrow x-3=9\)
hay x=12
2 tháng 9 2021
a: Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{x-\sqrt{x}-1}{x-2\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+2}{\sqrt{x}+1}-\dfrac{x-5}{x-\sqrt{x}-2}\right)\)
\(=\dfrac{x-x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-2\right)}:\dfrac{x-4-x+5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{1}\)
\(=\dfrac{x+2\sqrt{x}+1}{\sqrt{x}}\)
Bài 4:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
b) Ta có: \(AE\cdot AB=AF\cdot AC\)(cmt)
nên \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)