Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A=\(2^2-9^3+4^{-2}.16-2.5^2\)
\(=4-729+1-50=-774\)
B=\(\left(2^3.2\right).\dfrac{1}{2}+3^{-2}.3^2-7.1+5\)
\(B=2^4.\dfrac{1}{2}+1-7+5=8+1-7+5=7\)

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow\dfrac{A}{3}=\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow A-\dfrac{A}{3}=\dfrac{2A}{3}=\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\dfrac{2A}{3}=\left(\dfrac{1}{3^2}-\dfrac{1}{3^2}\right)+\left(\dfrac{1}{3^3}-\dfrac{1}{3^3}\right)+...+\left(\dfrac{1}{3^{99}}-\dfrac{1}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)=\dfrac{1}{3}-\dfrac{1}{3^{100}}\)
\(\Rightarrow2A=3\cdot\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\text{A}=\dfrac{1-\dfrac{1}{3^{99}}}{2}\)
\(\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{2.3^{99}}< \dfrac{1}{2}\)

Cách 1: Tính giá trị từng biểu thức trong ngoặc
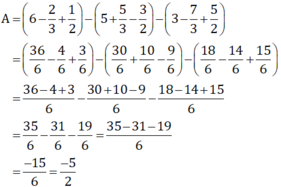
Cách 2: Bỏ dấu ngoặc rồi nhóm các số thích hợp
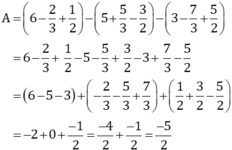

a) A = 120 : {60 : [(\(3^2+4^2\)) - 5]}
=120:[60:(25-5)]
=120 : (60 : 20)
= 120:3 = 40
b)B=\(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{6}\)
=\(\dfrac{3.6}{2.3.6}+\dfrac{2.6}{2.3.6}-\dfrac{2.3}{2.3.6}\)
=\(\dfrac{18+12-6}{36}=\dfrac{24}{36}=\dfrac{2}{3}\)
c) C = |4 - 6| + 2
=| -2 | +2
= 2 + 2 = 4
d) D= \(2^2+2^3+3^2+3^3-48\)
= \(2^2+2^3+3^2+3^3-2^4.3\)
= (\(2^2+2^3-2^4.3\)) +\(\left(3^2+3^3\right)\)
= \(2^2\left(1+2-2^2.3\right)+3^2\left(1+3\right)\)
= \(4\left(-9\right)+36\)= -36 + 36 =0
a) A= 120 : {60 : [(32 + 42 ) - 5 ]}
= 120 : { 60 : [ ( 9 + 16 ) - 5 ] }
= 120 : { 60 : [ 25 - 5 ] }
= 120 : { 60 : 20 }
= 120 : 3
= 40
b) \(B=\frac{1}{2}+\frac{1}{3}-\frac{1}{6}\)
\(B=\frac{1.3}{2.3}+\frac{1.2}{3.2}-\frac{1}{6}\)
\(B=\frac{3}{6}+\frac{2}{6}-\frac{1}{6}\)
\(B=\frac{3+2-1}{6}\)
\(B=\frac{4}{6}=\frac{2}{3}\)