Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

MB < MC => SABM < SACM => Điểm N là giao của đường thẳng d thỏa mãn đề bài với cạnh AC, nằm trong AC. Gọi I là trung điểm AC. Lúc đó SMNC = SBCI . Gọi P, Q tương ứng là hình chiều của I, N trên BC. => IP/NQ = BC/CM = CP/CQ . B, C, I, P cố định => xác định được Q từ đó tìm ra N.
????
Mình không hiểu câu trả lời của bạn Hà Chí Trung cho lắm

a) - Mô tả cách làm:
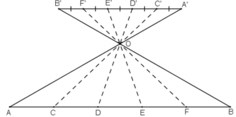
+ Vẽ đoạn thẳng PQ song song với AB, PQ có độ dài bằng 3 đơn vị.
+ E, F nằm trên PQ sao cho PE = EF = FQ = 1. Xác định giao điểm O của hai đoạn thẳng PB và QA
+ Vẽ các đường thẳng EO, FO cắt AB tại C và D.
Khi đó ta được AC = CD = DB.
- Chứng minh AC = CD = DB:
Theo hệ quả định lý Ta-let ta có:
ΔOAC có FQ // AC (F ∈ OC, Q ∈ OA) ⇒ 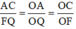
ΔOCD có EF // CD (E ∈ OD, F ∈ OC) ⇒ 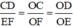
ΔODB có PE // BD (P ∈ OB, E ∈ OD) ⇒ 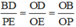
Từ 3 đẳng thức trên suy ra 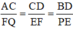
Mà FQ = EF = PE ⇒ AC = CD = DB (đpcm).
b) Tương tự chia đoạn thẳng AB thành 5 đoạn bằng nhau thực hiện như hình vẽ sau
Ngoài cách trên, ta có thể chia một đoạn thẳng thành 5 đoạn bằng nhau bằng cách vẽ thêm một đoạn thẳng AC bằng 5 đơn vị, chia đoạn thẳng AC thành 5 đoạn thẳng bằng nhau, mỗi đoạn bằng 1 đơn vị: AD = DE = EF = FG = GC.
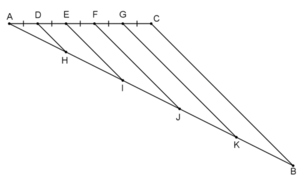
Từ các điểm D, E, F, G ta kẻ các đường thẳng song song với BC, cắt AB tại H, I, J, K. Khi đó ta thu được các đoạn thẳng AH = HI = IJ = JK = KB.

Qua A kẻ đường thẳng song song với DB, cắt BC ở E. Gọi M là trung điểm của EC, ta có đường thẳng DM là đường thẳng cần dựng.
Thật vậy S D C M = 1 2 S D C E = 1 2 S A B C
mỗi bn 3 k cho người giải dc