Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 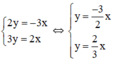
Xét (d): y = 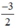 x có a =
x có a = 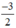 ; b = 0
; b = 0
(d’) : y = 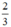 x có a’ =
x có a’ = 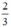 ; b’ = 0
; b’ = 0
Ta có: a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 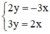 có nghiệm duy nhất.
có nghiệm duy nhất.

3 x = 6 2 y = - 7
Đường thẳng 3x = 6 song song với trục tung. Đường thẳng 2y = -7 cắt trục tung nên hai đường thẳng đó cắt nhau. Hệ phương trình có 1 nghiệm duy nhất

3 x + 5 y = 15 2 y = - 7 ⇔ y = - 3 5 x + 3 x = - 3 , 5
Ta có đường thẳng y = -3,5 song song với trục hoành
Đường thẳng y = - 3 5 x + 3 cắt trục hoành nên hai đường thẳng đó cắt nhau. Hệ phương trình có 1 nghiệm duy nhất

3 x = 6 x - 3 y = 2 ⇔ x = 2 y = 1 3 x - 2 3
Ta có đường thẳng x = 2 song song với trục tung. Đường thẳng y = 1 3 x - 2 3 cắt trục tung nên hai đường thẳng đó cắt nhau. Hệ phương trình có 1 nghiệm duy nhất.

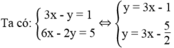
Vì hai đường thẳng có hệ số góc đều bằng 3 nhưng tung độ gốc khác nhau (-1 ≠ - 5/2 ) nên chúng song song với nhau.
Vậy hệ phương trình vô nghiệm.

Vì \(\dfrac{1}{-2}< >-\dfrac{2}{3}\) nên phương trình có nghiệm duy nhất

(II): 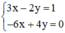
Xét: (d): 3x – 2y = 1 hay (d):
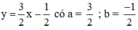
(d’): -6x + 4y = 0 hay (d’):
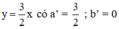
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (II) vô nghiệm.

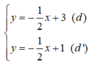
Xét (d): 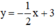 có a =
có a = 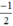 ; b = 3
; b = 3
(d’): 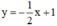 có a’ =
có a’ = 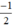 ; b’ = 1.
; b’ = 1.
Có a = a’; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ phương trình 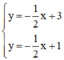 vô nghiệm
vô nghiệm