Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

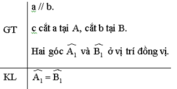
Chứng minh
Giả sử ∠(A1) ≠ ∠(B1)
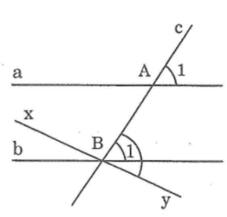
Qua B kẻ đường thẳng xy sao cho ∠(ABy) = ∠(A1)
Mà hai góc này ở vị trí so le trong nên theo dấu hiệu của hai đường thẳng song song, ta có xy //a
+) Qua điểm B ta kẻ được hai đường thẳng b và xy cùng song song với đường thẳng a. Theo tiên đề Ơ- clit suy ra đường thẳng xy trùng với đường thẳng b.

Ta có:
\(B_4=B_2\)(2 góc đối đỉnh)
\(B_4=A_2\)(2 góc so le trong)
\(\Rightarrow A_2=B_2\)
Ta có:
\(B_2=B_4\)(đối đỉnh)
\(B_2=A_4\)(so le trong)
\(\Rightarrow A_4=B_4\)
Ta có:
\(B_1=B_3\)(đối đỉnh)
\(B_3=A_1\)(so le trong)
\(\Rightarrow A_1=B_1\)
Ta có:
\(B_1=B_3\)(đối dỉnh)
\(B_1=A_3\)(so le trong)
\(\Rightarrow A_3=B_3\)
Ta Chứng minh được định lý:
Nếu 1 đường thẳng cắt 2 đường thẳng song song thì 2 góc đồng vị bằng nhau.


các đường thẳng và góc được biểu diễn trên hình vẽ:
Kẻ AH; BK vuông góc với đường thẳng a; b
Xét tam giác vuông ABH có: B2 + BAH = 90o
lại có góc BAH + A4 = 90o (do AH vuông góc với a)
=> góc A4 = B2 ; 2 góc này ở vị trí SLT
Ta có góc A2 = A4 ( đối đỉnh) => góc A2 = B2 ; 2 góc này ở vị trí đồng vị
Ta có góc A2 + A1 = 180o ( 2 góc kề bù)
=> góc B2 + A1 = 180o => chúng bù nhau
+) Từ 1 cặp góc SLT bằng nhau A4 = B2 ta suy ra được các cặp góc SLt ; đồng vị còn lại bằng nhau, trong cùng phía bù nhau ( bạn có thể xem ở mục Hình học lớp 7, đã có câu hỏi này)

ta giả sử rằng hai đường thẳng a và b là không song song với nhau :
khi đó a phải cắt b, ta gọi giao điểm của chúng là điểm O

Ta có \(\hept{\begin{cases}A_1=B_1\\B_1+B_2=180^0\end{cases}\Rightarrow A_1+B_2=180^0}\)
mà xét trong tam giác ABO có : \(A_1+B_2+O=180^0\Rightarrow O=0^0\) điều này là vô lý
vậy giả sử sai hay a phải song song với b

Cho 2 đường thẳng x và y song song với nhau
Đường thẳng d cắt x, y lần lượt tại A và B
Ta có x // y
=> \(\widehat{xAB}+\widehat{yBA}=180^o\) (Hai góc trong cùng phía)
Mà \(\widehat{yBA}+\widehat{yBd}=180^o\)(2 góc kề bù)
Nên \(\widehat{xAB}=\widehat{yBd}\)(đpcm)
Đây là 2 góc nằm ở vị trí đồng vị