PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
23 tháng 5 2019
Hàm số cho bằng bảng
Ví dụ:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 | 9 |
- Hàm số cho bằng công thức:
Ví dụ:
PT
1
CM
15 tháng 6 2019
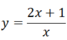
+ Để chứng minh những mệnh đề liên quan đến số tự nhiên n ∈ N* là đúng với mọi n mà không thể thử trực tiếp được thì ta làm như sau:
Bước 1: Kiểm tra mệnh đề đúng với n = 1 .
Bước 2: Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k ≥ 1. Chứng minh rằng nó cũng đúng với n = k+1.
Bước 3: Kết luận mệnh đề đúng với n ∈ N*.
+ Ví dụ: Chứng minh rằng với mọi n ∈ N* ta có: n3 + 5n chia hết cho 6.
Chứng minh: Đặt P(n) = n3 + 5n.
Với n =1 ⇒ P(1) = 6 ⋮ 6
Giả sử (Pn) chia hết cho 6 đúng với n=k ≥1, nghĩa là, ta có:
P(k) = (k3 + 5k) ⋮ 6.
Ta có: P(k+1) = (k+1)3 + 5(k+1) = k3 + 3k2 + 3k + 1 + 5k + 5 = k3 + 5k + 3(k2 + k) + 6
Mặt khác, theo giả thiết quy nạp ta có: k3 + 5k ⋮6.
Hơn nữa k2 + k = k(k+1) : 2 ( hai số tự nhiên tiếp k, k +1 phải có một số chẵn do k(k+1):2).
Do vậy P(k+1)⋮6. Tức mệnh đề đúng với n = k + 1.
Theo nguyên lí quy nạp, ta có P(n) = n3 + 5n chia hết cho 6 với mọi n ∈ N*.
CM
9 tháng 8 2019
Giả sử có hai cấp số cộng (un) với công sai d1 và (vn) với công sai d2.
Xét dãy (an) với an = un + vn
Ta có: an + 1 – an = (un + 1 + vn + 1) – (un + vn)
= (un + d1 + vn + d2) – (un + vn)
= d1 + d2 = const
⇒(an) là cấp số cộng với công sai d1 + d2.
Ví dụ:
CSC (un): 1; 4; 7; 10; 13; 16; 19; …. có công sai d1 = 3 ;
CSC (vn): 4 ; 6 ; 8 ; 10 ; 12 ; 14 ; 16 … có công sai d2 = 2.
⇒ (an): 5; 10; 15; 20; 25; 30; 35; … có công sai d = 5.
CM
28 tháng 6 2018
Giả sử có hai cấp số nhân (un) với công bội q1 và (vn) với công bội q2.
Xét dãy số (an) với an = un.vn với mọi n ∈ N*.
Ta có:
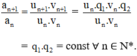
⇒ (an) là cấp số nhân với công bội q1.q2.
Ví dụ:
+ CSN (un) : 2 ; 4 ; 8 ; 16 ; 32 ; 64 ; … có công bội q1 = 2.
+ CSN (vn) : -1 ; 1 ; -1 ; 1 ; -1 ; 1 ; … có công bội q2 = -1.
⇒ CSN (an) : -2 ; 4 ; -8 ; 16 ; -32 ; 64 ; … có công bội q = -2.
MH
9 tháng 4 2017
Gọi (un) và (an) là hai cấp số cộng có công sai lần lượt là \(d_1\) và d2 và có cùng n số hạng.
Ta có:
un = u1 + (n -1) d1
an = a1 + (n – 1)d2
⇒ un + an = u1 + a1 + (n – 1).(d1 + d2)
Vậy un + an là cấp số cộng có số hạng đầu là u1 + a1 và công sai là d1 + d2
Ví dụ:
1, 3, 5, 7 ,.... là cấp số cộng có công sai d1 = 2
0, 5, 10, 15,.... là cấp số cộng có công sai d2 = 5
⇒ 1, 8, 15, 22 ,... là cấp số cộng có công sai là d = d1 + d2 = 2 + 5 = 7
MH
9 tháng 4 2017
an= a1. q1n-1, q1 là hằng số
bn= \(b_1q_2^{n-1}\), q2 là hằng số
Khi đó: an.bn = = a1. q1n-1. b1. q1n-1 = (a1b1)(q1q2)n-1
Vậy dãy số anbn là một cấp số nhân có công bội : q = q1q2
Ví dụ:
1, 2, 4 ,... là cấp số nhân có công bội q1 = 2
3, 9, 27, .... là cấp số nhân có công bội q2 = 3
⇒ Suy ra: 3, 8, 108.. là cấp số nhân có công bội: q = q1q2 = 2.3 = 6
- Nếu k là một hằng số thì (ku)’ = ku’
Thật vậy, ta có: (ku)' = k'u + ku' = 0.u + ku' = ku'
Do đạo hàm của hàm hằng bằng 0