Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(sin57^0=cos\left(90^0-57^0\right)=cos33^0\)
\(cos43^032'\) ko cần biến đổi vì góc đã thỏa mãn
\(tan72^015'=cot\left(90^0-72^015'\right)=cot\left(17^045'\right)\)
\(cot\left(85^035'\right)=tan\left(90^0-85^035'\right)=tan\left(4^025'\right)\)

sin75=cos15
cos53=sin37
tan71=cot19
cot47=tan43
sin57 độ 25'=cos 32 độ 35'
tan 68 độ35'=cot 21 độ 25'
cos 87 độ 12 p=sin 2 độ 48'

sin 55độ=cos 35độ
cos 63độ=sin 27độ
sin 80độ 15p=cos 9độ 45p
tan 87độ=cotg 3độ
cotg 82độ 43p= tan 7độ 17p

Bài 1:
\(\cos60^0=\sin30^0;\sin67^0=\cos23^0;\tan80^0=\cot10^0;\cot20^0=\cot20^0\)
Bài 2:
Xét tam giác ABC vuông tại A
\(a,\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{AC}{AB}=\tan\alpha\\ \cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{1}{\dfrac{\sin\alpha}{\cos\alpha}}=\dfrac{\cos\alpha}{\sin\alpha}\\ \tan\alpha\cdot\cot\alpha=\dfrac{AC}{AB}\cdot\dfrac{AB}{AC}=1\\ b,\sin^2\alpha+\cos^2\alpha=\dfrac{AC^2}{BC^2}+\dfrac{AB^2}{BC^2}=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\left(định.lí.pytago\right)\)

Vì 75 ° + 15 ° = 90 ° nên sin 75 ° = cos 15 °
Vì 53 ° + 37 ° = 90 ° nên cos 53 ° = sin 37 °
Vì 47 ° 20 ' + 42 ° 40 ' = 90 ° nên sin 47 ° 20 ' = cos 42 ° 40 '
Vì 62 ° + 28 ° = 90 ° nên tg 62 ° = cotg 28 °
Vì 82 ° 45 ' + 7 ° 15 ' = 90 ° nên cotg 82 ° 45 ' = tg 7 ° 15 '
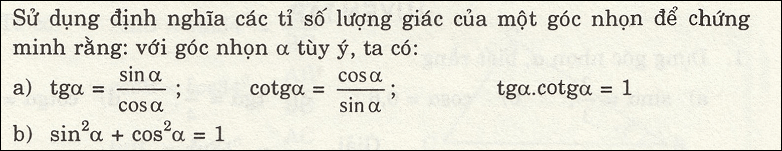
a) \(sin57^0=cos33^0\)
b) \(cos43^032'=sin46^028'\)
c) \(tan72^052'=cot17^08'\)
d) \(cot85^035'=tan4^025'\)