Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cứ 1 hạt nhân \(_{92}^{238}U\) bị phân rã tạo ra 1 hạt nhân \(_{82}^{206}Pb\). Từ đó ta có nhận xét là số hạt nhân \(_{92}^{238}U\) bị phân rã chính bằng số hạt nhân \(_{82}^{206}Pb\) tạo thành.
Tỉ số giữa số hạt nhân \(_{92}^{238}U\) bị phân rã và số hạt nhân \(_{92}^{238}U\) còn lại là
\(\frac{\Delta N}{N}= \frac{6,239.10^{18}}{1,188.10^{20}}= 0,0525 = \frac{1-2^{-\frac{t}{T}}}{2^{-\frac{t}{T}}}\)
Nhân chéo => \(2^{-\frac{t}{T}}= 0,95.\)
=> \(t = -T\ln_2 0,95 = 3,3.10^8\)(năm)
=> Tuổi của khối đã là 3,3.108 năm.

Đáp án D

⇔ 6 , 239 . 10 18 1 , 188 . 10 20 = 2 - t 4 , 47 . 10 9
=> t = 3,3.108 năm

Gọi N 0 là số hạt nhân urani lúc ban đầu ; N t là số hạt nhản urani lúc t mà ta nghiên cứu : N t = 1,188. 10 20 hạt = 118,8. 10 18 hạt ; số hạt nhân chì lúc t là : N 0 - N t = 6,239. 10 18 hạt.
Từ đó suy ra : N 0 = (6,239 + 118,8). 10 18 hạt = 125,039. 10 18 hạt
Mặt khác, ta lại
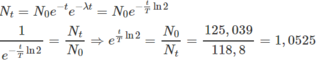
Lấy log Nê-pe hai vế, ta được :
t/T .ln2 = 0,051183 ⇒ t = 0,07238T = 0,3301. 10 9
Tuổi của khối đá là t = 3,3. 10 8 năm.

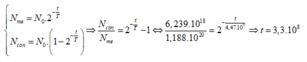

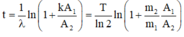
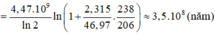
Chọn B.
Gọi N0 là số hạt U chứa trong khối đá lúc mới hình thành, t là tuổi của khối đá.
Số hạt U còn lại đến thời điểm phát hiện ra = N 0 2 1 T
Số hạt chỉ tạo thành = số hạt U đã phân rã = N 0 1 − 2 1 T
Tỉ số giữa hai hạt này ở thừi điểm phát hiện là: 1 , 188.10 20 6 , 239.10 18 = 2 1 4 , 47.10 9 1 − 2 1 4 , 47.10 9 ⇒ t ≈ 3 , 3.10 8 n ă m