

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(_1^1p + _4^9Be \rightarrow _2^4He + _3^6X\)
Áp dụng định luật bảo toàn động lượng \(\overrightarrow P_p+0 =\overrightarrow P_{He}+ \overrightarrow P_{X} \)(hạt nhân Be đứng yên)
Dựa vào hình vẽ ta có
\(P_{p}^2+ P_{He}^2 = P_X^2\)
=> \(2m_{p}K_{p}+2m_{He} K_{He} = 2m_{X}K_{X}. \)
=> \(K_{p}+4K_{He} = 6K_{X} => K_X = 3,575MeV.\)
Áp dụng định luật bảo toàn năng lượng toàn phần (hạt nhân Be đứng yên)
\(K_{p}+m_{p}c^2+m_{Be}c^2 = K_{He} + m_{He}c^2+ K_{X}+m_{X}c^2\)
=> \((m_p-m_{He}-m_{X})c^2= K_{He}+K_X-K_p= 2,125MeV\)
Như vậy năng lượng tỏa ra của phản ứng chính bằng hiệu động năng của các hạt sau phản ứng cho động năng của các hạt trước phản ứng và bằng 2,125 MeV.

Đáp án A
Phương pháp: Định luật bảo toàn năng lượng và bảo toàn động lượng trong phản ứng hát nhân
Cách giải :
Phương trình phản ứng ![]()
Áp dụng định luật bảo toàn năng lượng toàn phần và định luật bảo toàn động lượng ta có
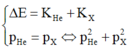
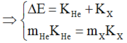
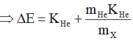
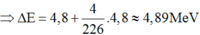

Đáp án A
Phương trình phản ứng:
R
88
226
a
→
H
2
4
e
+
X
86
224
Áp dụng định luật bảo toàn năng lượng toàn phần và định luật bảo toàn động lượng ta có 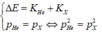
p 2 = 2 K m
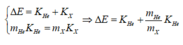
⇒ ∆ E = 4 , 8 + 4 226 . 4 , 8 ≈ 4 , 8 M e V

Đáp án D
Phương trình phản ứng: R 88 226 a → H 2 4 e + X 86 224
Áp dụng định luật bảo toàn năng lượng toàn phần và định luật bảo toàn động lượng ta có

⇒ ∆ E = 4 , 8 + 4 226 . 4 , 8 ≈ 4 , 89 M e V

Đáp án D
Theo định luật bảo toàn số khối ta có X có khối lượng 6u.
Vì hạt bay ra có phương vuông góc với p ban đầu, áp dụng định luật bảo toàn động lượng cho ta
P x 2 = P α 2 + P P 2 ; mà ta cũng có p 2 = 2 m k nên
m X K x = m α K α + m P K P ⇒ K X = 3 , 575
Từ định luật bảo toàn năng lượng toàn phần và định nghĩa năng lượng tỏa ra ta có năng lượng tỏa ra
W t = K X + K α - K P = 3 , 575 + - 5 , 45 = 2 , 125 M e V