Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ko thể dịch nổi đề câu 1 a;b, chỉ đoán thôi. Còn câu 2 thì thực sự là chẳng hiểu bạn viết cái gì nữa? Chưa bao giờ thấy kí hiệu tích phân đi kèm kiểu đó
Câu 1:
a/ \(\int\frac{2x+4}{x^2+4x-5}dx=\int\frac{d\left(x^2+4x-5\right)}{x^2+4x-5}=ln\left|x^2+4x-5\right|+C\)
b/ \(\int\frac{1}{x.lnx}dx\)
Đặt \(t=lnx\Rightarrow dt=\frac{dx}{x}\)
\(\Rightarrow I=\int\frac{dt}{t}=ln\left|t\right|+C=ln\left|lnx\right|+C\)
c/ \(I=\int x.sin\frac{x}{2}dx\)
Đặt \(\left\{{}\begin{matrix}u=x\\dv=sin\frac{x}{2}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=-2cos\frac{x}{2}\end{matrix}\right.\)
\(\Rightarrow I=-2x.cos\frac{x}{2}+2\int cos\frac{x}{2}dx=-2x.cos\frac{x}{2}+4sin\frac{x}{2}+C\)
d/ Đặt \(\left\{{}\begin{matrix}u=ln\left(2x\right)\\dv=x^3dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{2dx}{2x}=\frac{dx}{x}\\v=\frac{1}{4}x^4\end{matrix}\right.\)
\(\Rightarrow I=\frac{1}{4}x^4.ln\left(2x\right)-\frac{1}{4}\int x^3dx=\frac{1}{4}x^4.ln\left(2x\right)-\frac{1}{16}x^4+C\)

\(0\le sin^2x\le1\)
\(\Rightarrow2\le y\le3\)
\(y_{min}=2\) khi \(sinx=0\Rightarrow x=k\pi\)
\(y_{max}=3\) khi \(sin^2x=1\Leftrightarrow x=\frac{\pi}{2}+k\pi\)

y ' = - 3 x 2 + 2 ( 2 m + 1 ) x - m 2 + 3 m - 2
Để hàm số đã cho có cực đại, cực tiểu nằm về hai phía so với trục tung khi và chỉ khi phương trình y’ = 0 có hai nghiệm x 1 , x 2 trái dấu.
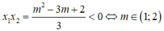
Chọn A

Giao điểm với trục tung B(0 ;-1). Ta có
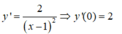
Hệ số góc của tiếp tuyến của đồ thị hàm số 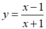 tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
Chọn B

Lời giải:
Giả sử tiếp điểm có hoành độ $x_0$. Phương tình tiếp tuyến tại tiếp điểm là:
\(y=f'(x_0)(x-x_0)+f(x_0)=\frac{-x}{(x_0-1)^2}+\frac{2x_0^2-2x_0+1}{(x_0-1)^2}\) (\(\Delta\))
Khoảng cách từ \(\Delta\) đến \(I(1,2)\) là :
\(d=\frac{\left | \frac{-1}{(x_0-1)^2}-2+\frac{2x_0^2-2x_0+1}{(x_0-1)^2} \right |}{\sqrt{\frac{1}{(x_0-1)^4}+1}}=\sqrt{2}\Rightarrow x_0\in\left \{0;2 \right \}\)
Do đó có 2 PTTT là:\(\left\{\begin{matrix}y=-x+1\\ y=-x+5\end{matrix}\right.\)