Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C.
Gợi ý: Loại A, D vì tập xác định của hàm số là 25 - x 2 ≥ 0 ⇔ -5 ≤ x ≤ 5.
Loại B, vì
x |
-5 |
0 |
y |
0 |
5 |

Lời giải:
$y'=\frac{2x}{\sqrt{2x^2+1}}$
$y'>0\Leftrightarrow 2x>0\Leftrightarrow x>0$ hay $x\in (0;+\infty)$
$y'< 0\Leftrightarrow 2x< 0\Leftrightarrow x\in (-\infty;0)$
Vậy hàm số đồng biến trên $(0;+\infty)$ và nghịch biến trên $(-\infty; 0)$
Đáp án A.

Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 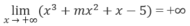
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.

Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 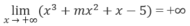
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.
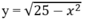 nghịch biến trên khoảng:
nghịch biến trên khoảng:
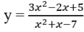
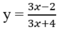 luôn nghịch biến;
luôn nghịch biến;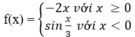
Đáp án: C.
Gợi ý: Loại A, D vì tập xác định của hàm số là 25 - x 2 ≥ 0 ⇔ -5 ≤ x ≤ 5.
Loại B, vì