Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x, y (km/h) lần lượt là vận tốc của xe thứ nhất và xe thứ hai. Điều kiện: x > 0, y > 0.
Vì hai xe khởi hành đồng thời và đi ngược chiều nhau, sau 10 giờ chúng gặp nhau nên ta có:
10x + 10y = 750
Vì xe thứ nhất khởi hành trước xe thứ hai 3 giờ 45 phút thì sau khi xe thứ hai đi được 8 giờ chúng gặp nhau nên thời gian xe thứ nhất đi được là:
3 giờ 45 phút + 8 giờ = 11 giờ 45 phút = 11(3/4) = 47/4 giờ
Ta có phương trình: (47/4)x + 8y = 750
Ta có hệ phương trình:
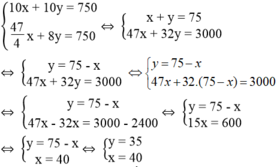
Giá trị của x và y thỏa điều kiện bài toán.
Vậy vận tốc của xe thứ nhất là 40 km/h, vận tốc của xe thứ hai là 35 km/h.

Gọi vận tốc xe t1 là x (x>0) (km/h)
vận tốc xe t2 là y (y>0) (km/h)
Hai xe khởi hành cùng lúc và đi ngược chiều nhau,sau 10h thì gặp ,ta có pt: \(10x+10y=750\left(1\right)\)
Xe 1 khởi hành trc xe 2 3h45p,xe 2 đi đc 8h thì gặp thì khi gặp nhau xe 1 đi được 11h45p = 47/4h
Ta có pt: \(\frac{47}{4}x+8y=750\left(2\right)\)
từ (1) và (2), ta có hệ: \(\hept{\begin{cases}10x+10y=750\\\frac{47}{4}x+8y=750\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=75\\47x+32y=3000\end{cases}}}\)
Giải hệ ta đc: x=40,y=35 (TMĐK)
Vậy...

Đổi 3 giờ 45 phút = 3,75 giờ
Gọi vận tốc xe lửa thứ nhất là x (km/h) (x > 0)
Gọi vận tốc xe lửa thứ hai là y (km/h) (y >0)
Quãng đường xe lửa thứ nhất đi trong 10 giờ là: 10x (km)
Quãng đường xe lửa thứ hai đi trong 10 giờ là: 10y (km)
Vì hai xe đi ngược chiều và gặp nhau nên ta có pt: 10x + 10y = 750 (1)
Vì xe thứ nhất khởi hành trước xe thứ hai 3 giờ 45 phút nên khi gặp nhau thì thời gian xe thứ nhất đã đi là: 8 + 3,75 = 11,75 (giờ)
Quãng đường xe thứ nhất đã đi là: 11,75x (km)
Quãng đường xe thứ hai đã đi là: 8y (km)
Ta có pt: 11,75x + 8y = 750 (2)
Từ (1) và (2) ta có hệ pt:
Đối chiếu với ĐK ta có x = 40; y = 35 đều thỏa mãn điều kiện
Vậy vận tốc xe thứ nhất là 40 km/h; Vận tốc xe lửa thứ hai là 35 km/h

Đổi 2h40ph=8/3 giờ
Gọi vận tốc xe thứ nhất là x (km/h), vận tốc xe thứ hai là y (km/h) với x;y>0
Do 2 xe đi ngược chiều gặp nhau sau 3 giờ nên: \(x+y=\dfrac{120}{3}=40\)
Quãng đường xe thứ nhất đi được sau 2h40ph: \(\dfrac{8x}{3}\) (km)
Quãng đường còn lại: \(120-\dfrac{8x}{3}\)
Do hai xe gặp nhau khi xe thứ 2 đi được 1 giờ nên:
\(x+y=\left(120-\dfrac{8x}{3}\right):1\Leftrightarrow\dfrac{11x}{3}+y=120\)
Ta được hệ: \(\left\{{}\begin{matrix}x+y=40\\\dfrac{11x}{3}+y=120\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=30\\y=10\end{matrix}\right.\)

Bạn tích dùng cho mình đi không biết mình có giải đúng không nếu bạn cho là mình làm đúng thì tích đi mình sẽ giải ngay sau đó

Đổi: 1h 6 phút = 1,1 giờ; 2 giờ 30 phút = 2,5 giờ
Gọi vận tốc của xe ô tô đi từ A là x ; vận tốc của xe ô tô đi từ B là y ( >0; km/h)
+) Nếu cùng khởi hành sau hai giờ chúng gặp nhau.
Sau hai giờ ô tô đi từ A đi được quãng đường là: 2x ( km)
Sau hai giờ ô tô đi từ B đi được quãng đường là: 2 y ( km)
=> Có phương trình : 2x + 2y = 220 ( km) (1)
+) Nếu xe đi từ A khởi hành trước xe đi từ B 1, 1 giờ:
Sau 2,5 h xe đi từ A đi được quãng đường là: 2,5.x ( km)
Xe đi từ B đi được quãng đường là: ( 2,5 - 1,1) .y= 1,4y (km)
=> Có phương trình: 2,5x + 1,4y - 220 (km) (2)
Từ (1) và (2) ta có hệ : \(\hept{\begin{cases}2x+2y=220\\2,5x+1,4y=220\end{cases}}\Leftrightarrow\hept{\begin{cases}x=60\\y=50\end{cases}}\) ( thỏa mãn)
Vậy...
xe lửa đi từ a vận tốc là : 35km
xe lửa đi từ b vận tốc là : 30 km