Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời gian vật 1 đi hết 1 vòng tròn nhỏ:
t1= \(\frac{C_1}{v_1}=\frac{50}{4}\)= 12,5 (s).
Thời gian vật thứ hai đi hết một vòng tròn lớn là:
t2= \(\frac{C_2}{v_2}=\frac{80}{8}\) = 10 (s).
Giả sử sau khi vật thứ nhất đi được x vòng và vật thứ hai đi được y vòng thì hai vật lại cùng nằm trên một bán kính của vòng tròn lớn.
Ta có: T là thời gian chuyển động của hai vật.
T = t1.x = t2.y =>\(\frac{x}{y}=\frac{t_2}{t_1}=\frac{10}{12,5}=\frac{4}{5}\)
Mà x, y phải nguyên dương và nhỏ nhất do đó ta chọn x=4 và y=5.
Nên thời gian chuyển động của hai vật là: T = t1.x= 12,5.4= 50 (s).

Em thứ nhất chạy nhanh hơn em thứ hai nên trong thời gian t0 = 1s em thứ nhất chạy hơn em thứ hai một đoạn đường là:
s = s1 – s2 = v1.t0 – v2.t0 = 4,8.1 – 4.1 = 0,8m.
Sau khoảng thời gian t (s), quãng đường em thứ nhất chạy hơn em thứ hai là:
S = 0,8.t
Em thứ nhất sẽ gặp em thứ hai lần đầu tiên sau thời gian t (s) khi mà quảng đường em thứ nhất chạy hơn em thứ hai trong khoảng thời gian đó bằng đúng chu vi một vòng chạy.
Khi đó ta có: S = 0,8.t = Cchu vi = 400 m
Suy ra (v1 – v2).t = 400.
Vậy thời gian ngắn nhất để hai em gặp nhau trên đường chạy là:
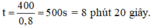

a, áp dụng ct: \(2\pi R=2.3,14.\dfrac{250}{1000}=1,57km\)
\(=>S1=32,5t\left(km\right)\)
\(=>S2=35t\left(km\right)\)
\(=< pt:32,5t+1,57=35t=>t=0,628h\approx38'\)
đổi \(4h30'=270'\)
vậy lần đầu 2 xe gặp nhau lúc \(4h30'+38'\approx5h8'\)
b, \(=>\)gọi số lần gặp nhau là x (lần) \(\left(x\in N,x>0\right)\)
=>số lần gặp nhau \(x=\dfrac{1,5}{0,628}\approx2,3\)
kết hợp điều kiện \(=>x\approx2\) lần

bán kính đường ytib điing tâm thật là vận tốc lớp 8 ko dậy :))

ta có:
v1+v2=8/5
\(\Leftrightarrow v_1+v_2=1.6\)(1)
nếu vận tốc xe một lớn hơn xe hai thì:
v1-v2=6/10=0.6(2)
giải một và hai ta có:v1=1.1;v2=0.5
nếu vận tốc xe hai lớn hơn xe một thì v1=0.5;v2=1.1

R = 250 m = 0,25 km
Chiều dài của trường đua chính là chu vi của hình tròn bán kính 0,25km
s = π.2.R=3,14 . 2 . 0,25= 1,57km
khi bắt đầu xuất phát tại 1 điểm, vì 2 xe di chuyển cùng chiều nên khoảng cách 2 xe chính là độ dài của trường đua
Thời gian để 2 xe gặp nhau lần 1 kể từ lúc xuất phát là:
t = \(\frac{s}{v_2-v_1}=\frac{1,57}{35-32,5}=0,628\left(h\right)=38\left(p\right)\)
vậy lần gặp đầu tiên của 2 xe vào lúc 5h8p
Quãng đường xe 1 đi được trong thời gian t là:
s1 = v1.t = 0,628 . 32,5 = 20,41 (km)
Quãng đường xe 2 đi trong thời gian t là:
s2 = v2.t = 0,628 . 35 = 21,98 (km)
b) từ câu a ta có, khi 2 xe xuất phát từ 1 điểm thì cứ sau t = 0,628 h thì lại gặp nhau 1 lần,
Vậy số lần gặp nhau trong 1,5 h là:
n = \(\frac{1,5}{0,628}=2,4\left(l\text{ần}\right)\)
Vì n ϵ Nnên n chỉ có thể = 2Vậy trong 1,5 h 2 xe gặp nhau 2 lần
)